2.7 Trabajos escolares
Gnomon
Consiste en un tablero rectangular de unos 70 x 50 cm que se va a colocar en el suelo horizontal de forma que sus lados largos queden paralelos a la línea Este-Oeste. En el eje central Norte-Sur, a unos 10 cm del borde Sur, se coloca un clavo (u otro objeto similar) de unos 10 cm de altura; es interesante que acabe en punta para que el extremo de su sombra esté bien definido.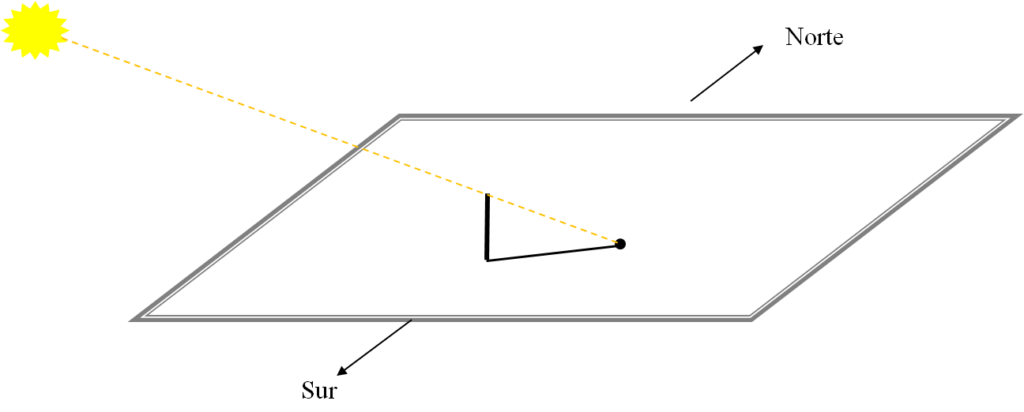
La superficie del tablero debe permitir dibujar en ella; una solución simple es que el tablero sea de madera y sobre él se sujete (por ejemplo con chinchetas) una cartulina.
Sin mover para nada el gnomon se va señalando en él el extremo de la sombra del clavo a lo largo de todo un día, digamos de hora en hora.
Es interesante repetir la experiencia en diferentes fechas del año, especialmente en las más señaladas desde el punto de vista astronómico (solsticios y equinoccios); para que todo resulte bien es muy importante que el gnomon esté siempre en la misma posición; para conseguirlo lo más seguro es marcar en el suelo (en el patio de recreo) los bordes del tablero.
Otra actividad interesante consiste en anotar la hora y la longitud de la sombra, elaborar una gráfica con esos datos y analizarla.
O también, conociendo la altura del clavo y la longitud de la sombra en un momento dado averiguar el ángulo de elevación (la altura) del Sol sobre el horizonte, completar una tabla con horas y alturas, hacer una gráfica con esos datos y estudiarla.Cuadrante
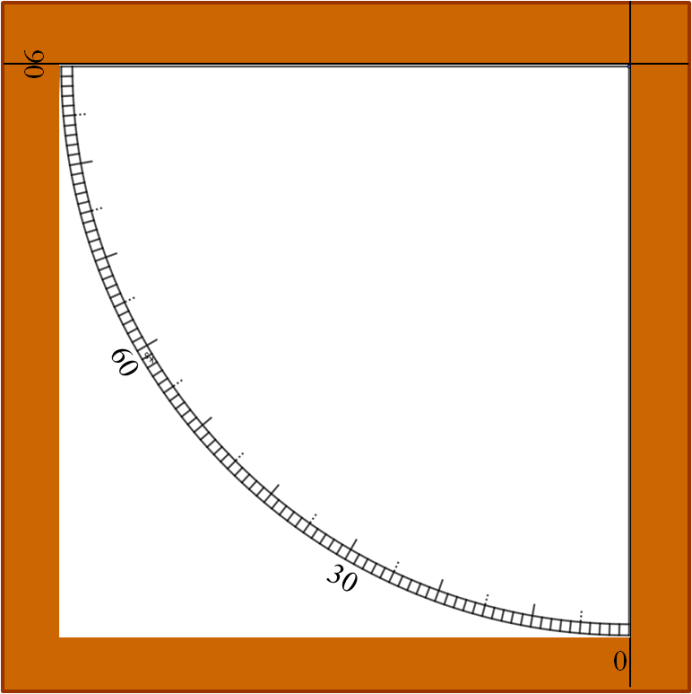
En un tablero de madera fina pero rígida (es útil el DM, de 5 mm de grosor por ejemplo) de unos 25×25 cm se dibujan dos rectas paralelas a los bordes, a unos 2 cm, como se muestra en el dibujo. Luego se dibuja o se pega un cuarto de círculo graduado (haz clic aquí para ver o imprimir uno) ajustado a las dos líneas antes dibujadas y graduado como se indica: 0º abajo y 90º en el extremo superior.
En el borde superior del tablero hay que situar algún sistema para hacer puntería. 
Pueden ser un par de hembrillas (como la de la foto), el tubo de un bolígrafo pegado a lo largo del borde, o lo que se te ocurra.
Luego tienes que hacer un agujero fino (con un clavo, por ejemplo, no hace falta emplear el taladro) justo en el vértice, pasar por ese agujero una cuerda fina que va a ser nuestra plomada, utilizando como peso lo que tengamos a mano: una tuerca, un tornillo algo pesado.
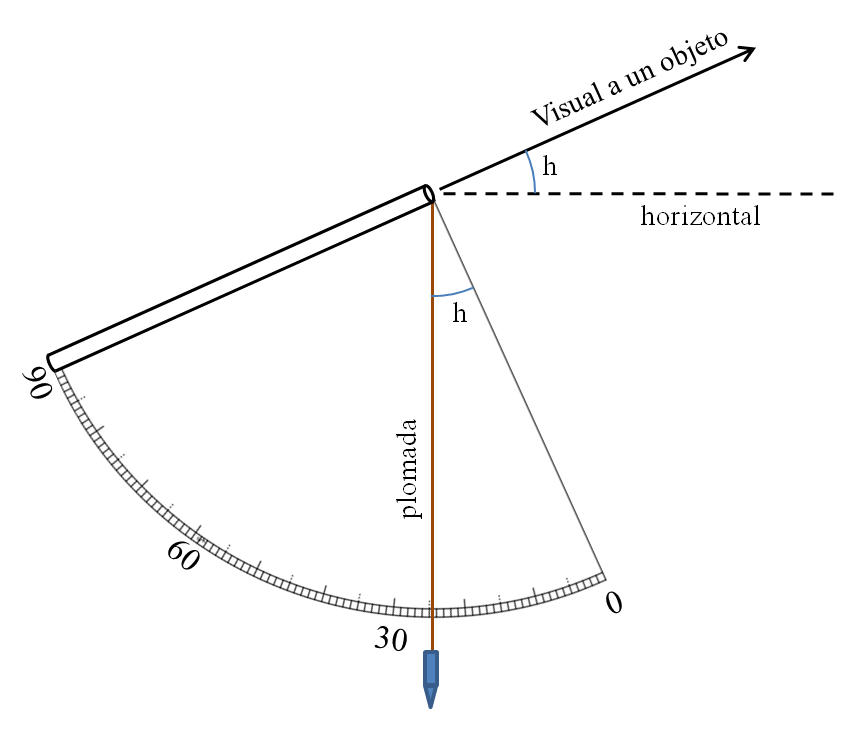
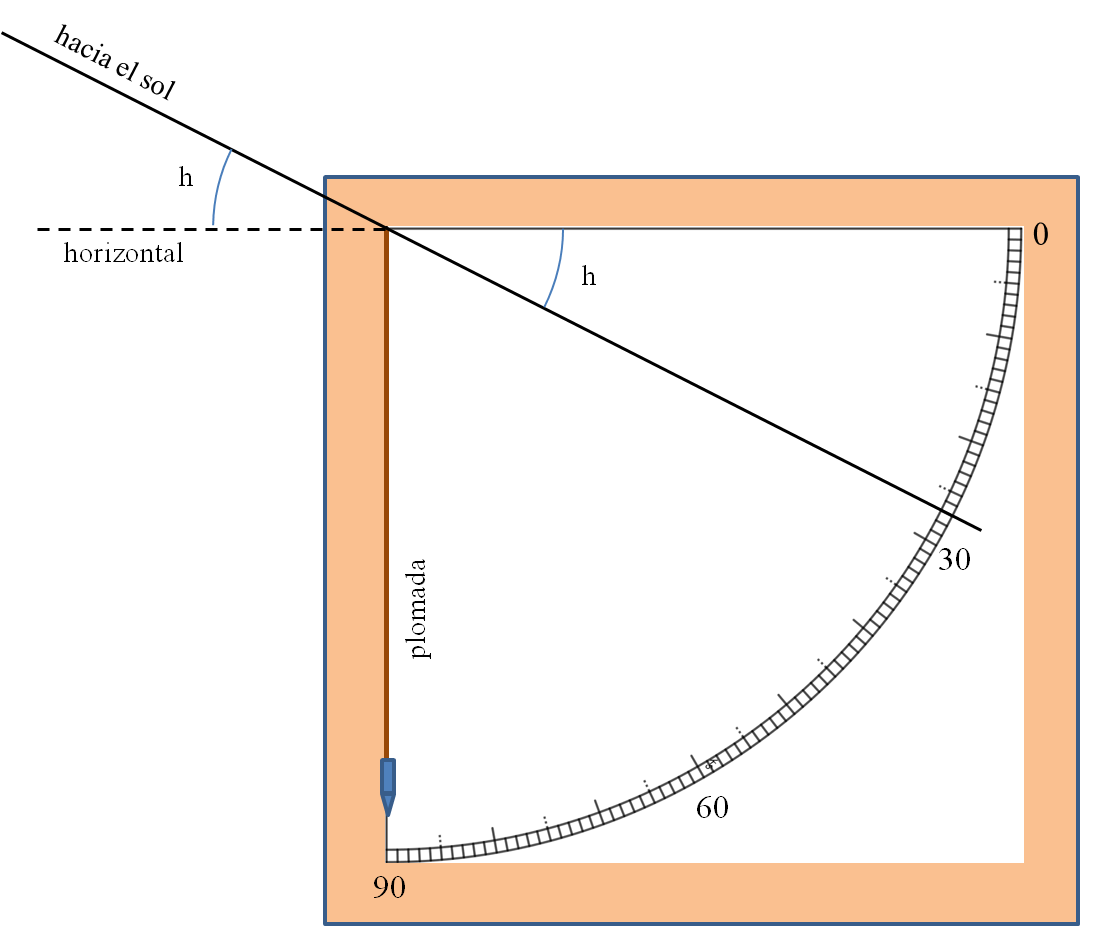
Ya tenemos armado nuestro cuadrante. Para utilizarlo se inclina lo que haga falta hasta que apuntemos a un objeto celeste (o terrestre). La plomada indicará en el cuarto de círculo gra-duado precisamente la altura h de ese objeto, porque los dos ángulos indicados como h en la figura tienen que ser iguales.
Teodolito
Aquí tienes otras imágenes de teodolitos “caseros” que pueden servirte de orientación si te decides a construir uno. Los círculos o semicírculos graduados y transparentes que puedes encontrar en una papelería suelen ser muy útiles.
Instituto de secundaria Las Viñas de Manilva, en Málaga.
http://4.bp.blogspot.com/-ts8CE0AnEho/TZZCJu55THI/AAAAAAAAA3A/ZY36zTwzEEU/s1600/DSCI0013.JPG
El zócalo de Ptolomeo. 
Es un instrumento especialmente diseñado para medir las coordenadas horizontales del Sol. Consiste en un tablero cuadrado, pequeño (20×20 cm por ejemplo) pero grueso (podría ser aglomerado de 19 mm), de manera que se mantenga vertical sin dificultad. Sobre una de las caras del tablero se dibuja un cuadrante, graduado desde 0° hasta 90°, y se coloca en su vértice un pequeño clavo que sobresalga. Haz clic aquí si quieres ver o imprimir un cuarto de círculo graduado.
Este tablero debe poder girar sobre una base en la que se pega un círculo completo graduado de 0 a 360°. Haz clic aquí si quieres ver o imprimir un círculo completo graduado. Hay que colocar la base de forma que quede perfectamente orientada, con la graduación 0° en dirección N y la 180° hacia el S. Un clavo situado en el centro de la base puede servir de eje de giro del tablero vertical.
Se mueve el tablero vertical (girándolo sobre su eje) hasta que apunte exactamente hacia el Sol, lo que se consigue cuando las dos caras del tablero están en sombra. En esa posición se puede leer el acimut en la graduación del círculo dibujado en la base.
También sirve para medir la altura del Sol, es decir el ángulo que forman sus rayos con la horizontal. Para ello se mueve el tablero vertical, hasta que la luz del Sol entre ligeramente en la cara con el cuadrante dibujado y la sombra del clavo sea muy larga y alcance la graduación (fotografía). El valor señalado por la sombra del clavo es precisamente la altura del Sol. La plomada solo sirve para verificar que el cuarto de círculo esté bien nivelado, con un borde vertical.
Trazado de la meridiana
Procedimiento clásico
Se coloca un palo vertical en un punto central G del suelo donde se va a realizar esta práctica, generalmente un patio del centro escolar. Conviene que este “gnomon” sea bastante alto, como por ejemplo de 1 m, que termine en forma de punta fina (para que el extremo de su sombra pueda precisarse lo mejor posible) y que esté bien vertical comprobándolo con una plomada.
Se dibuja una circunferencia de centro G y un radio de por lo menos 3 m. Cuanto mayor sea el radio más preciso será el procedimiento, pero hay que asegurarse de que la sombra del gnomon alcance esa circunferencia en todo momento. Puede haber edificios próximos que constituyan un obstáculo.
Se espera hasta que, por la mañana, la sombra del gnomon alcance a la circunferencia y se marca el punto (A). Luego hay que repetir la operación por la tarde, señalando en el suelo el punto (A’) en el que la sombra vuelve a tocar la circunferencia.
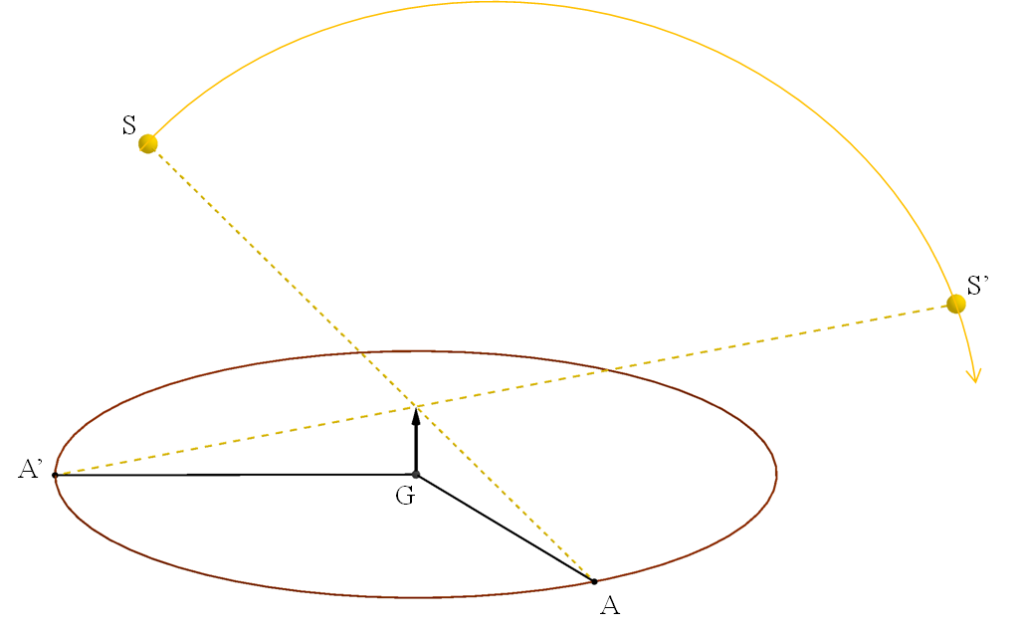
Puesto que las sombras GA y GA’ miden lo mismo, las dos posiciones del Sol (S y S’) tienen la misma altura sobre el horizonte y son simétricas con respecto al punto central de su trayectoria (la culminación, cuando se sitúa exactamente sobre el punto cardinal Sur).
Por lo tanto la mediatriz del segmento AA’ será la línea meridiana Norte – Sur. Basta con marcar el punto medio (M) del segmento AA’ y unirlo con G. Esa recta MG será la meridiana.
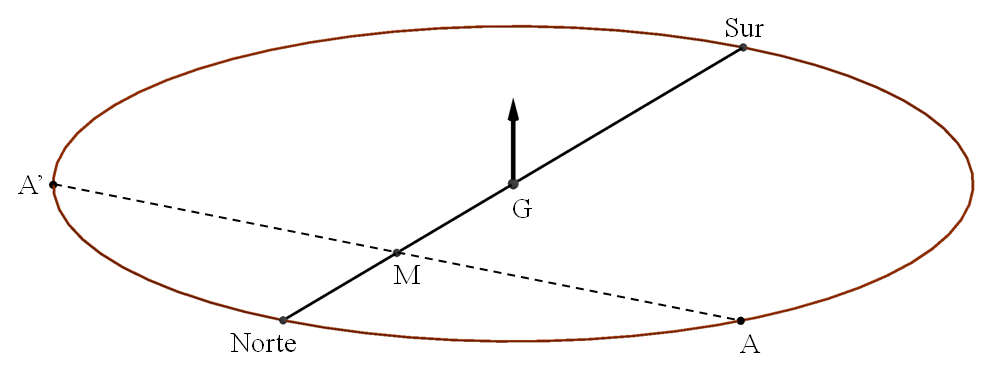
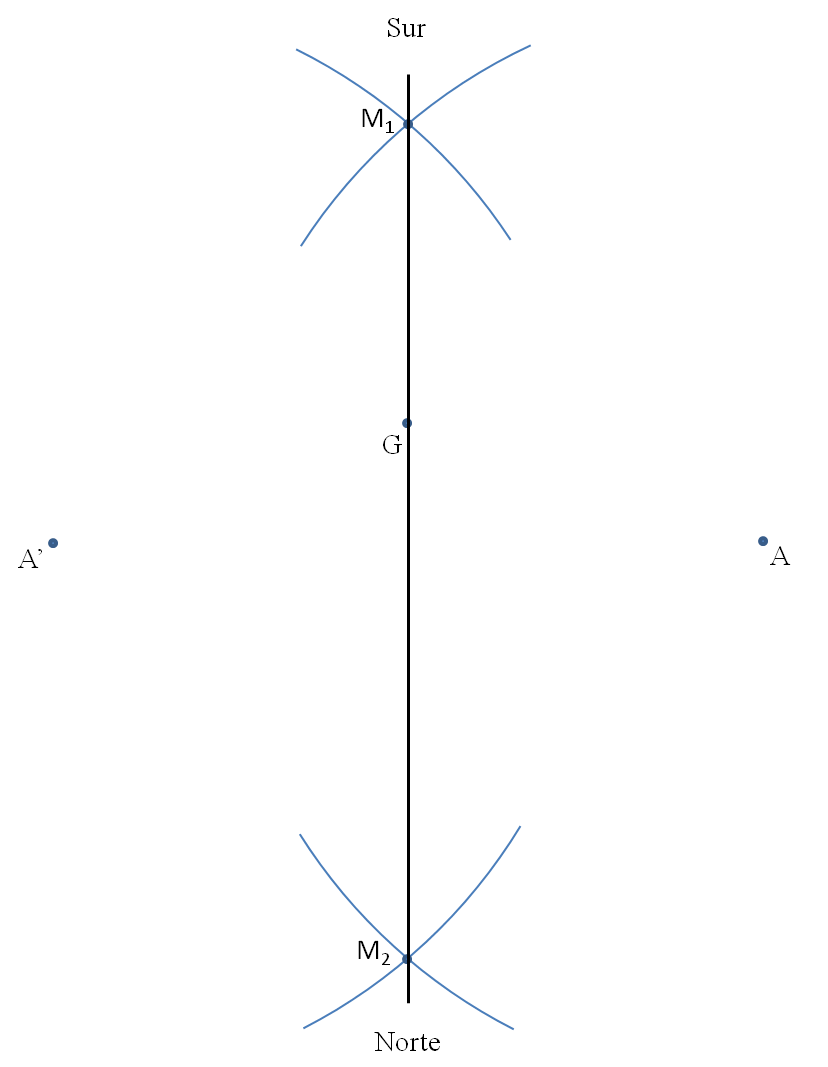
El trazado de la mediatriz puede mejorarse mediante el procedimiento clásico en dibujo. Con centro en A y en A’ y con el mismo radio (lo mayor posible) se trazan pequeños arcos de circunferencia en la zona previsible donde vaya a situarse la mediatriz. Se obtienen así dos puntos M1 y M2 más distanciados y que marcarán la posición de la meridiana con mejor precisión que los excesivamente próximos G y M.
Procedimiento práctico
Para este segundo método es preciso conocer con la máxima exactitud posible la longitud geográfica del lugar de observación. Puede obtenerse de algún mapa muy detallado (escala 1:25.000 o aún menor) o mediante algún programa informático como el Google maps.
Una vez conocida la longitud geográfica es necesario obtener la hora exacta del mediodía solar verdadero (cuando el acimut del Sol es justamente de 180º) en ese lugar y para la fecha elegida. Se puede conseguir también mediante algún software que simule los movimientos celestes, como el Stellarium. Es recomendable hacerlo en fechas próximas al solsticio de invierno, en diciembre o enero, cuando la altura del Sol a mediodía sea muy baja y, por tanto, las sombras se proyecten con mayor longitud. Y poner en hora nuestros relojes (con las señales horarias de la radio, por ejemplo) el día elegido por la mañana.
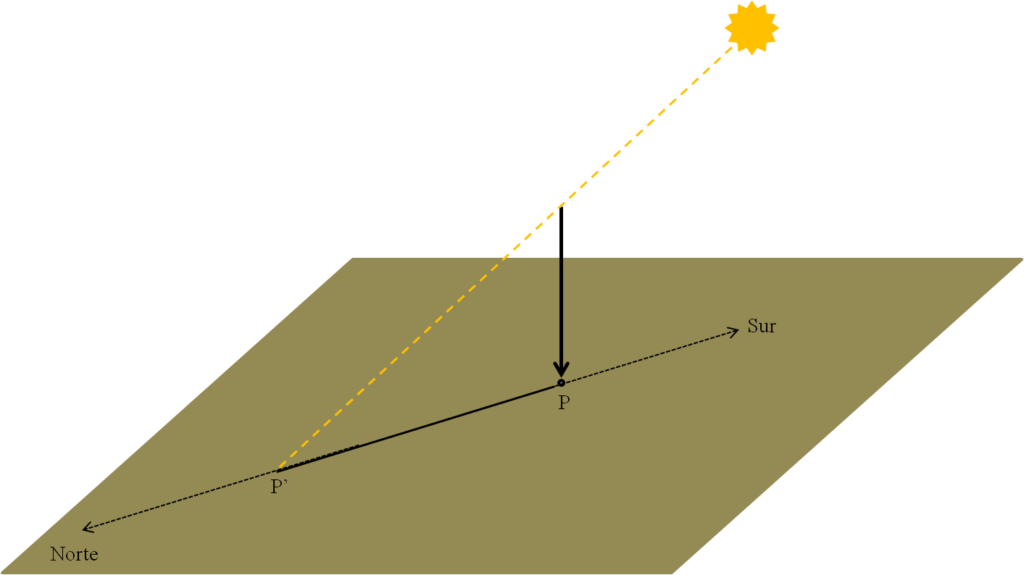
Hay que conseguir una plomada de bastante longitud, digamos unos 2 m. Se puede sujetar mediante una escalera, suspenderla en alguna canasta de baloncesto que tengamos a mano o como nos parezca.
Una vez colocada y estabilizada la plomada se señala en el suelo el punto que queda justo debajo de ella (P). Esperamos hasta que llegue a la hora del mediodía. En ese preciso momento se marca en el suelo el extremo de la sombra de la plomada (P’). La línea PP’ será nuestra meridiana.
