Como la Tierra es, muy aproximadamente, esférica, se ha podido establecer un sistema bastante sencillo que permite situar cualquier punto sobre su superficie. En una esfera perfecta, ideal, en principio no hay ningún elemento, ningún punto que destaque de forma natural (piensa, por ejemplo, en una bola de billar sin ninguna marca). En una naranja sí que lo hay: el punto que la une a la rama del árbol. Pues en el planeta Tierra también hay dos puntos, los polos, que destacan de manera natural al ser los extremos de su eje de rotación, y el plano central, el ecuador, es el que utilizaremos ahora como referencia privilegiada.

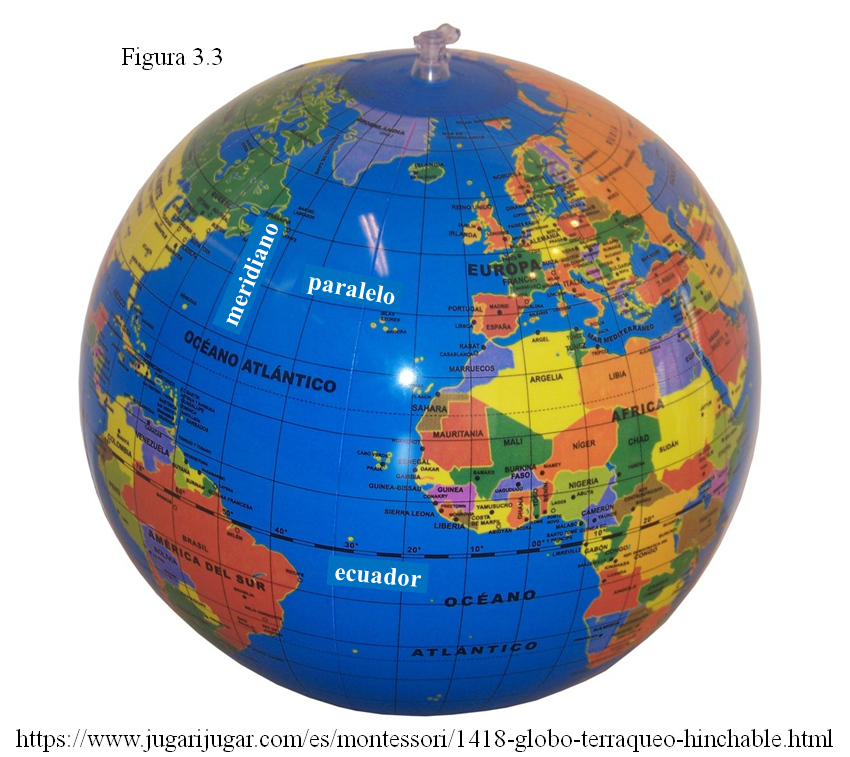
En este globo terráqueo se aprecia la red de paralelos y meridianos que permiten definir la posición de cualquier punto de la superficie.

La siguiente figura es una representación de la Tierra. PN y PS son los polos y G el centro. Los círculos máximos que pasan por los dos polos son meridianos. El círculo máximo perpendicular al eje terrestre por G es el ecuador. Los círculos más pequeños paralelos al ecuador se llaman así: paralelos.

Se ha señalado un punto O cualquiera de la superficie terrestre, así como el meridiano y el paralelo que pasan por él. La posición de O queda determinada por su paralelo y su meridiano, y recíprocamente, un paralelo y un meridiano definen con exactitud la situación de un punto sobre la superficie de la Tierra. Se definen así dos coordenadas: la latitud y la longitud.

La latitud de O es la distancia angular entre el ecuador y el paralelo que pasa por O. También se puede definir como el ángulo φ que forma la línea GO con el plano del ecuador. Los valores de φ pueden variar entre 0^º (para un punto en el ecuador) y 90^º (para el polo) y pueden ser norte o sur. La latitud de Madrid es de unos 40^º norte, la de Barcelona 41^º 30′ norte, mientras que Buenos Aires está a unos 35^º de latitud sur.

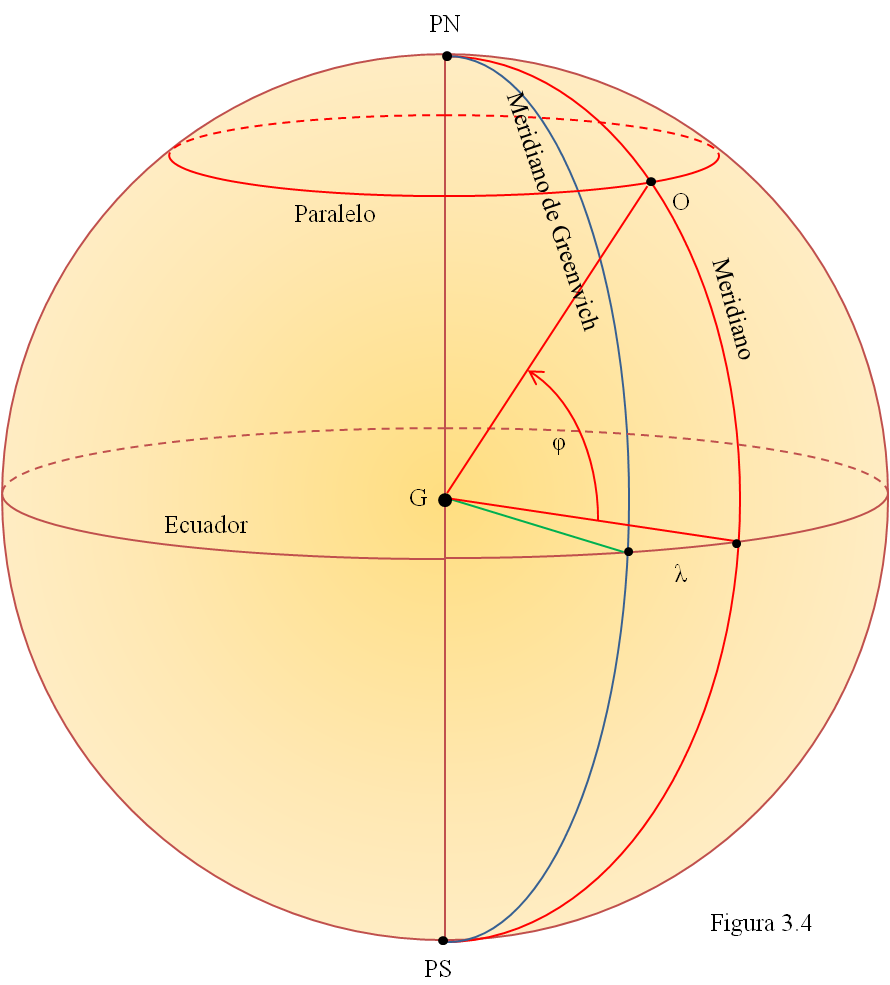
Para definir la segunda coordenada, la longitud, necesitamos escoger arbitrariamente un meridiano como origen, como meridiano 0, puesto que no hay ninguno que destaque de forma natural. Por convención, el elegido es el de Greenwich, localidad cercana a Londres en la que se construyó en el siglo XVII uno de los primeros observatorios astronómicos del mundo. La longitud λ del punto O es la distancia angular entre el meridiano de Greenwich y el que pasa por O. λ puede oscilar entre 0^º (para un punto situado justo en el meridiano de Greenwich, como Castellón o el Monte Perdido en los Pirineos) y 180^º (para un punto situado en el lado opuesto de la Tierra, como el extremo oriental de Siberia), y puede ser este (como Alemania) u oeste (como Portugal).

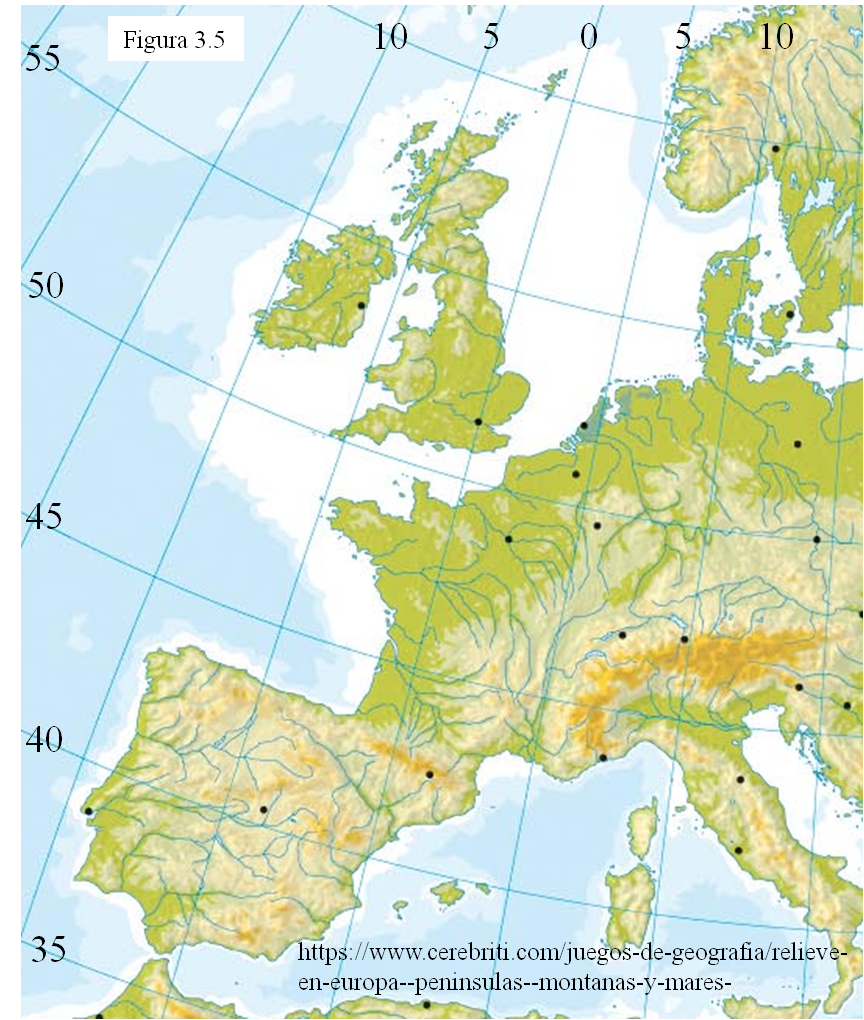
Este es un mapa de Europa con algunos meridianos y paralelos señalados. Las latitudes son siempre Norte, pero las longitudes pueden ser Este u Oeste. Por ejemplo, Londres está en el meridiano 0 y entre los paralelos 50 y 55; su latitud es de unos 51º 30’ y su longitud es 0º, claro. En cambio Lisboa está un poco por debajo del paralelo 40º y casi en el meridiano 10º Oeste, así que tiene una latitud de unos 39º y su longitud aproximada es 9º Oeste.

Hay una capital con φ = 49º Norte y λ = 2º Este; se trata de París.

Por otra parte, con φ = 56º Norte y λ = 12º 30’ Este, nos encontramos con la capital de Dinamarca, Copenhague.