3.4 Mapas de constelaciones
Esta tabla recoge las coordenadas y la magnitud de las principales estrellas de la Osa Mayor.
| Estrella | Ascensión Recta α | Declinación δ | Magnitud |
| β (Merak) | 11h 00m | 56o 30′ | 2 |
| α (Dubhe) | 11h 03m | 62o 00′ | 2 |
| γ (Phecda) | 11h 55m | 54o 00′ | 2 |
| δ (Megrez) | 12h 15m | 57o 00′ | 3 |
| ε (Alioth) | 12h 55m | 56o 00’ | 2 |
| ζ (Mizar) | 13h 25m | 55o 00′ | 2 |
| η (Alkaid) | 13h 45m | 49o 30′ | 2 |
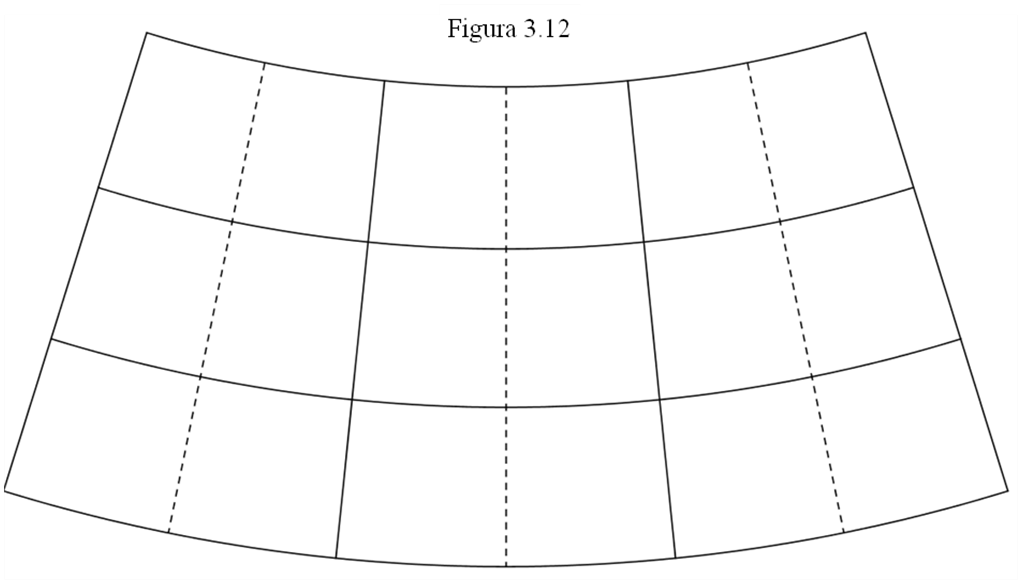
La lámina es una retícula con unos cuantos arcos de circunferencia y unas rectas, más o menos verticales, que parecen converger por la parte de arriba (el punto de convergencia sería el polo norte celeste). Los arcos de circunferencia son paralelos de declinación y están trazadas de 5 en 5º. Las otras líneas representan los meridianos de ascensión recta.
Haz clic aquí para imprimirla.
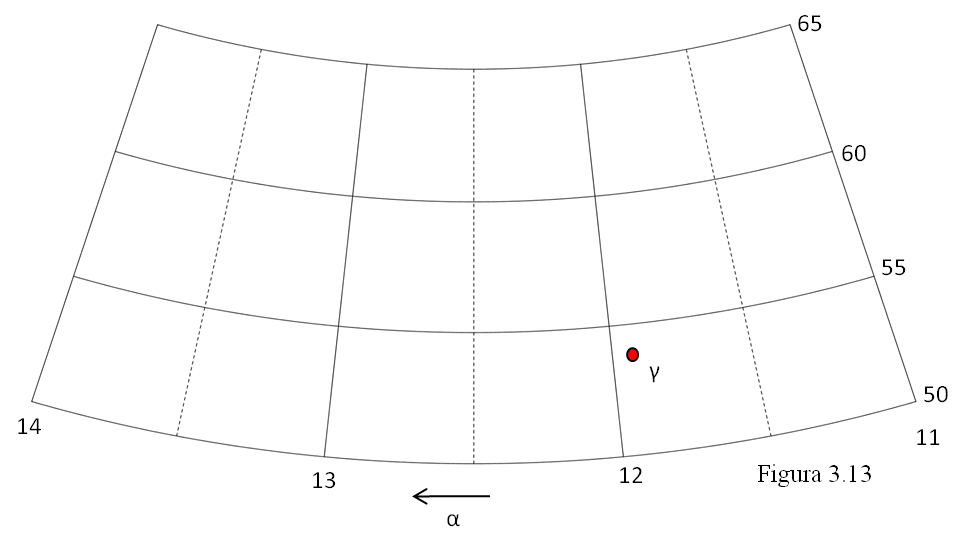
Lo primero que vas a hacer es graduar los paralelos y los meridianos en función de los valores que aparecen en la tabla. Fíjate primero en la declinación de las estrellas de la Osa Mayor. ¿Cuál es el menor valor de la declinación δ en la tabla? ¿Y el mayor? Para graduar los paralelos escribe a la derecha del inferior 50º, 55º en el siguiente, hasta 65º en el más alto.
Vamos con los meridianos. Los que están dibujados con trazo continuo corresponden a una hora exacta de ascensión recta; los dibujados con trazo discontinuo son de media hora (30 minutos). Los valores de α que hay en la tabla están entre 11 y 14 horas. Ten cuidado: el primer meridiano es el de la derecha. Señala en él 11h; luego 12h, 13h y 14h en el meridiano de la izquierda. Así, el meridiano central, será el de las 12h 30m, el único que es del todo vertical.
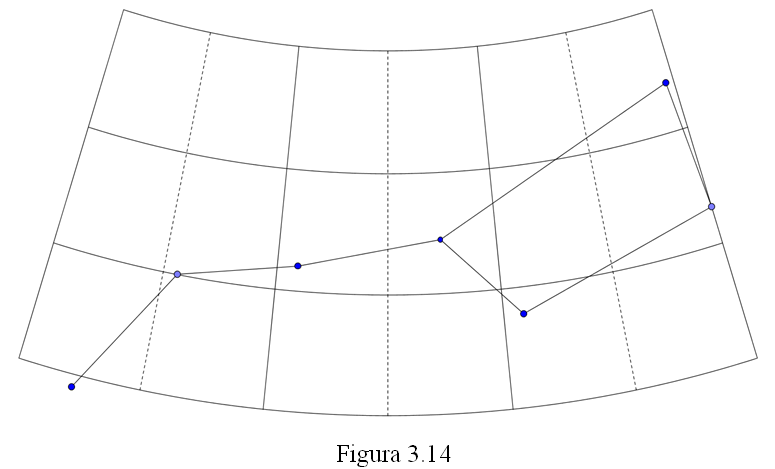
Sitúa ahora, aproximadamente, cada estrella de la tabla en su posición en la retícula conforme a sus coordenadas. Ten presente la magnitud. Dibuja un pequeño círculo para las de 2ª magnitud y haz un poco más pequeña la de 3ª. Escribe la letra griega de cada estrella para poder detectar y subsanar fácilmente cualquier error cometido al situarla. En esta figura aparece en su lugar la estrella γ. Tienes que obtener la figura conocida de la Osa Mayor. Si no fuera así revisa la posición de las estrellas que no te encajen. Une las estrellas con líneas como ya sabes.
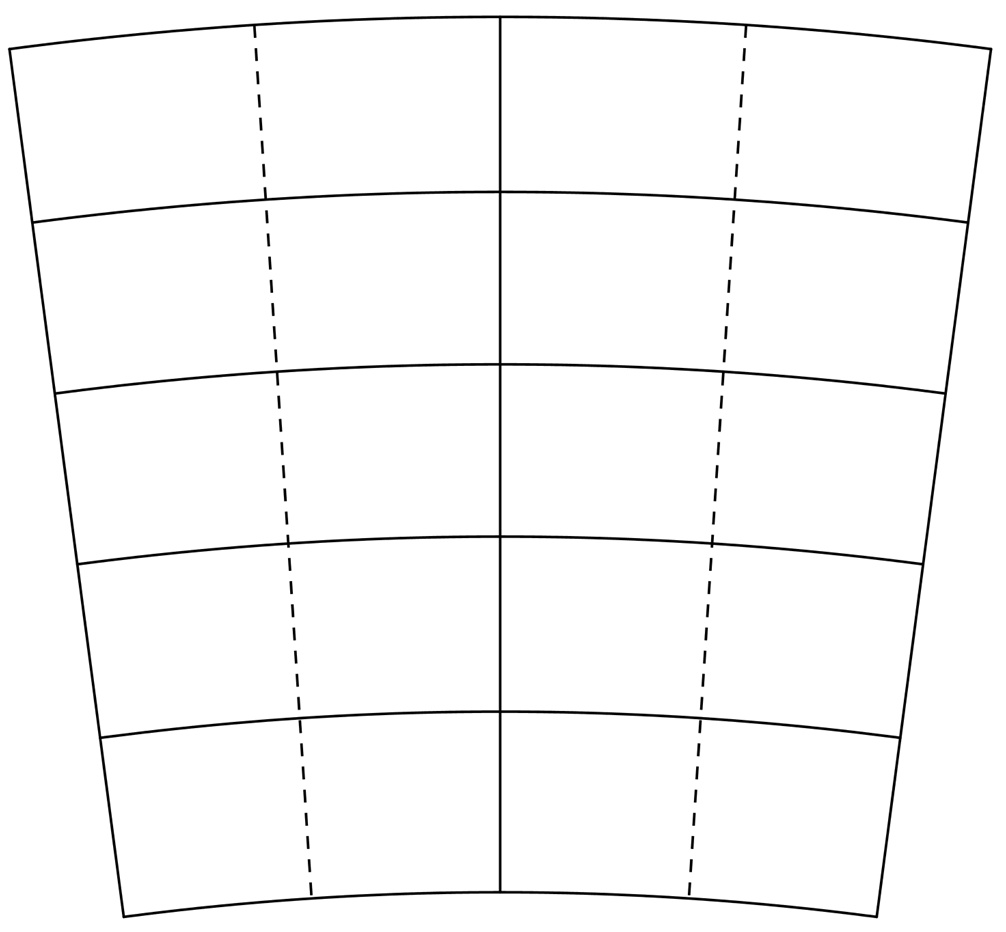
Ejercicio 3.2
Gradúa y completa los mapas de Orión y Escorpio utilizando las cuadrículas y las tablas siguientes. Ten cuidado con la graduación de la declinación en la de Escorpio que está en el hemisferio sur (el polo Sur estaría debajo). Para imprimir la cuadrícula de Orión haz clic aquí y para Escorpio aquí
ORIÓN
| Estrella | A.R. | DEC. | MAG. | Estrella | A.R. | DEC. | MAG. | |
| β (Rigel) | 5h 01m | -8o 00’ | 0 | λ | 5h 30m | +10o 00’ | 3 | |
| γ (Bellatrix) | 5h 25m | +6o 30’ | 2 | δ | 5h 30m | -0o 30’ | 2 | |
| ε | 5h 35m | -1o 15’ | 2 | ζ | 5h 40m | -2o 00’ | 2 | |
| χ | 5h 45m | -9o 40’ | 2 | α (Betelgeuse) | 5h 55m | +7o 25’ | 0 |
SCORPIO
| Estrella | A.R. | DEC. | MAG. | Estrella | A.R. | DEC. | MAG. | |
| ß | 16h 05m | -20o 00’ | 3 | δ | 16h 00’ | -22o 30’ | 2 | |
| π | 15h 59m | -26o 00’ | 3 | ρ | 15h 57’ | -29o 00’ | 4 | |
| α (Antares) | 16h 29m | -26o 30’ | 1 | σ | 16h 21’ | -25o 30’ | 3 | |
| τ | 16h 36m | -28o 00’ | 3 | σ | 16h 50’ | -34o 00’ | 2 | |
| µ | 16h 52m | -38o 00’ | 3 | ζ | 16h 55’ | -42o 30’ | 3 | |
| η | 17h 12m | -43o 00’ | 3 | λ | 17h 32’ | -37o 00’ | 2 | |
| θ | 17h 36m | -43o 00’ | 2 | κ | 17h 41’ | -39o 00’ | 2 |
Haz clic aquí para ver la solución
Ejercicio 3.3
- Con ayuda del planisferio averigua, aproximadamente, las coordenadas del centro de las siguientes constelaciones: Auriga, Hércules, Cuervo, Pegaso y Capricornio.
- Identifica los objetos (estrellas u objetos telescópicos señalados con la letra M) cuya posición viene dada por las coordenadas siguientes:
| A.R. | DEC. | ¿Objeto? | |
| A | 10h 10m | 12º | |
| B | 18h 52m | 25º | |
| C | 00h 41m | 41º | |
| D | 18h 35m | 38º | |
| E | 12h 40m | 12º |
Haz clic aquí para ver la solución.
Ejercicio 3.4
Haz el dibujo de la constelación de Sagitario. Fíjate que, al igual que Escorpio, está en el hemisferio Sur. Haz clic aquí para imprimir los meridianos y paralelos.
| Estrella | A.R. | DEC. | MAG. | Estrella | A.R. | DEC. | MAG. | |
| γ | 18h 05m | -30o 26’ | 3 | δ | 18h 20m | -29o 50’ | 3 | |
| ε | 18h 23m | -34o 24’ | 2 | λ | 18h 27m | -25o 27’ | 3 | |
| ψ | 18h 44m | -27o 01’ | 3 | σ (Nunki) | 18h 54m | -26o 19’ | 2 | |
| ζ | 19h 0m1 | -29o 54’ | 3 | τ | 19h 06m | -27o 42’ | 3 |
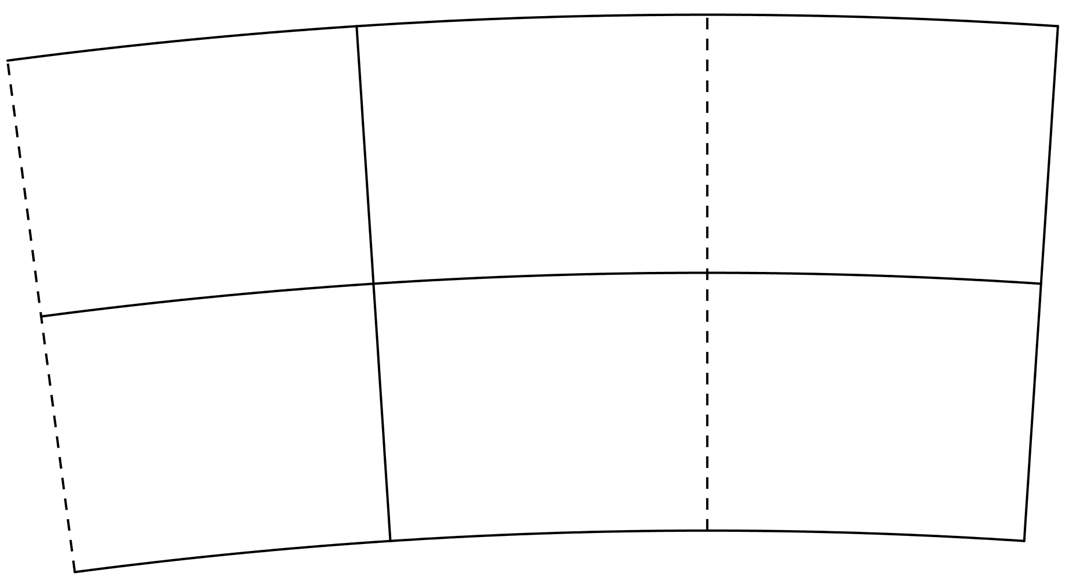
Haz clic aquí para ver la solución.
Ejercicio 3.5. La constelación fantasma
Aquí tienes una tabla como las anteriores, sólo que no sabemos a qué constelación corresponde. Gradúa la cuadrícula, haz clic aquí para imprimirla, y señala en ella las estrellas de la tabla. Obtendrás la figura de una conocida constelación. ¿Cuál es? ¿Cómo se llama su principal estrella? Ten en cuenta que es muy, muy brillante.
| Estrella | A.R. | DEC. | MAG. | Estrella | A.R. | DEC. | MAG. | |
| ß | 16h 20m | -8o 00’ | 2 | α | 16h 45m | -6o 30’ | 0 | |
| θ | 16h 55m | -2o 00’ | 4 | ι | 16h 56m | -7o 00’ | 4 | |
| γ | 17h 05m | -5o 30’ | 4 | ε | 17h 00m | -19o 00’ | 2 | |
| δ | 17h 10m | -16o 30’ | 2 | η | 17h 25m | -19o 15’ | 2 |
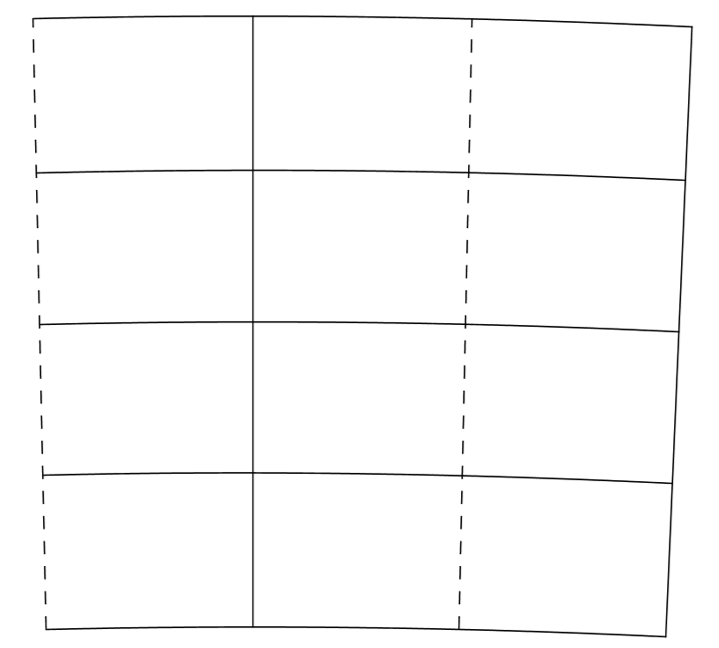
Haz clic aquí para ver la solución.
El dibujo se ajusta bastante bien a la visión que tenemos de esta constelación en el cielo, pero, si consultas el planisferio, verás que las coordenadas no coinciden. ¿Sabrías corregir la tabla para adjudicar a cada estrella sus verdaderas coordenadas?