Curso General de Astronomía
Tema 4. El modelo de las dos esferas
KEPLER. GRUPO DOCENTE DE ASTRONOMÍA
4.3 La latitud y la polar
¿Por qué hemos puesto antes el polo norte celeste P precisamente a 40° del punto cardinal norte N? Pues porque esa es la altura de la Polar vista desde un punto O sobre la Tierra en la posición de España y así hemos dibujado todas las figuras hasta ahora. ¿Qué pasaría si nos desplazásemos hacia el norte o hacia el sur? Fíjate en la figura 4.4 Al mover el punto O, el horizonte también variará y, asimismo, la distancia angular entre N y P.
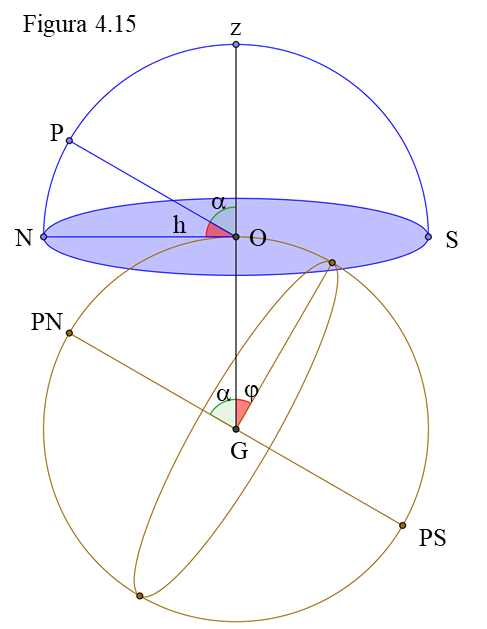
Hay una relación precisa entre la latitud del lugar O de observación y la altura del polo P respecto al horizonte. La figura 4.15 representa la esfera terrestre y la semiesfera celeste visible por encima del horizonte tal y como la ve un observador situado en un punto cualquiera O, cuya latitud es φ. La línea OP es la visual hacia el polo P, paralela al eje de la Tierra. El ángulo h es la altura del polo, el ángulo que hay que levantar la vista desde el horizonte para apuntar hacia la Polar (esa visual OP debe ser paralela al eje de la Tierra puesto que el Polo Norte celeste está en la prolongación del eje pero a distancia enorme). Por eso los ángulos α (sombreados en verde) tienen que ser iguales. Pero h = 90º – α (en la semiesfera celeste visible) y también φ = 90º – α (en la Tierra). Por tanto, los ángulos φ y h tienen que ser iguales: φ = h.
Esto es una demostración matemática rigurosa que nos permite enunciar un importante resultado teórico deducido del modelo de las dos esferas: la altura del polo sobre el horizonte es igual a la latitud del lugar de observación.
Este resultado teórico tiene muchas consecuencias. Aquí hablaremos de dos de ellas.
La primera es que tenemos a nuestra disposición un método práctico para calcular nuestra latitud: medir con algún instrumento adecuado, un cuadrante por ejemplo, la altura de la estrella Polar que está muy cerca del polo. Colón hizo esto para mantener sus naves siempre a 28° de latitud, midiendo por las noches la altura de “la estrella del norte” para confirmar que su posición era la correcta mientras se dirigían hacia América. Sólo muy recientemente se han sustituido los procedimientos astronómicos por otros (electrónicos, los famosos GPS) para poder calcular la posición de un punto en la Tierra.
La segunda consecuencia es que podemos simular cómo ven el movimiento de los astros en otros países, en otras latitudes, sin más que tener en cuenta la inclinación adecuada del eje respecto al horizonte. Haremos algunas simulaciones en el apartado siguiente.