10.6 Otros cuerpos menores
Cometas
Su aspecto visual (figura 10.46) consiste en un extremo brillante, la “coma” (la “cabeza”), seguida de una larga cola (“kometés” en griego significa “de larga cabellera”). Estas llamativas, breves y, sobre todo, inesperadas apariciones causaban un gran impacto y pánico generalizado siendo interpretadas como presagios de graves infortunios.
En realidad (figuras 10.47 y 10.48), son pequeños objetos irregulares (unos pocos kilómetros de tamaño) de órbitas muy excéntricas. Consisten en una “bola de nieve sucia” (80% de agua helada mezclada con monóxido de carbono CO, CO2, rocas). Cuando están muy lejos del Sol permanecen inactivos, congelados, pero al acercarse el calor hace que parte de sus hielos se sublimen (pasen directamente de sólido a gas) y formen la brillante cabellera o coma, que rodea al núcleo. El viento solar se encarga de expulsar (en la dirección opuesta al Sol) parte de esos gases formándose así la cola, de gran tamaño (hasta 100 millones de km) pero baja densidad, que es lo más espectacular de los cometas vistos desde la Tierra.
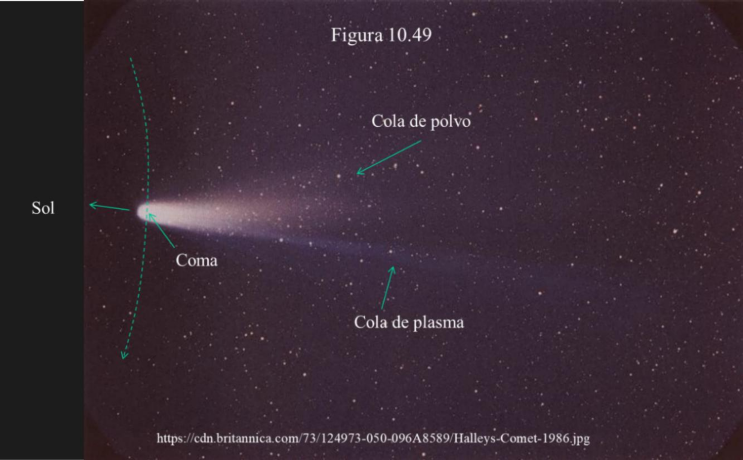
Suelen tener dos colas (figura 10.49), una recta, la de plasma, producida por partículas ionizadas dirigidas por el viento solar y otra, la de polvo, ligeramente curvada porque al alejarse del Sol esas motas de polvo pierden algo de velocidad (conforme a las leyes de Kepler) y se quedan atrás. Se clasifican en cometas de período corto (menor de 20 años, cuya órbita suele ser interior a la de Júpiter), medio (entre 20 y 200 años, como el Halley) y largo (mayor de 200 años). La mayoría tienen órbitas elípticas (con el Sol en un foco) y sus apariciones se suceden periódicamente (algunos cada pocos años, otros cada cientos de años) También los hay que sólo se hacen visibles una vez llevando órbitas abiertas (parábolas o hipérbolas).
En cada paso por su perihelio un cometa pierde parte de su materia por lo que se va gastando y puede terminar en un resto inactivo (que sería un asteroide), o bien puede morir estrellándose contra el Sol, un planeta o un satélite, o incluso ser capturado por algún planeta y convertirse en su satélite.
Esas motas de polvo que pierde el cometa cuando está activo, cerca de su perihelio, quedan en órbita en torno al Sol y si la Tierra en su curso anual atraviesa una zona en la que abundan esos restos se producen en la atmósfera frecuentes estrellas fugaces: es lo que se llama una “lluvia de estrellas”. En esta tabla tienes las más importantes.
| Nombre | Fecha | Cometa asociado |
| Perseidas | 12 agosto | Swift-Tuttle |
| Oriónidas | 21 octubre | Halley |
| Táuridas | 7 noviembre | Encke |
| Leónidas | 17 noviembre | 1866 I |
| Gemínidas | 13 diciembre | Faetón (cometa extinto) |
Los confines del sistema
Plutón (figura 10.50) fue considerado como planeta desde su descubrimiento en 1930 por un joven de 23 años, Clyde Tombaugh, desde el observatorio Flagstaff de Arizona. Sin embargo, su pequeño tamaño (menor que la Luna), su gran inclinación orbital y alta excentricidad le situaban muy al límite para tan alta dignidad. El descubrimiento en la década de 1990 de otros numerosos cuerpos con órbitas similares (a unas 40 UAs) fue decisivo y en 2006 la Unión Astronómica Internacional decidió incluir a Plutón en una nueva categoría: los planetas enanos.
Así pues, más allá de Neptuno nos encontramos con un nuevo conjunto disperso de cuerpos que forman el cinturón de Kuiper (figura 10.51) y que ocupa un enorme espacio entre 30 y 500 UAs. El cinturón principal se sitúa en el interior (30 – 50 UAs) donde están, entre otros, los objetos con órbitas similares a Plutón (y que por eso se denominan “plutinos”) y la inmensa zona exterior es mucho más dispersa aún.
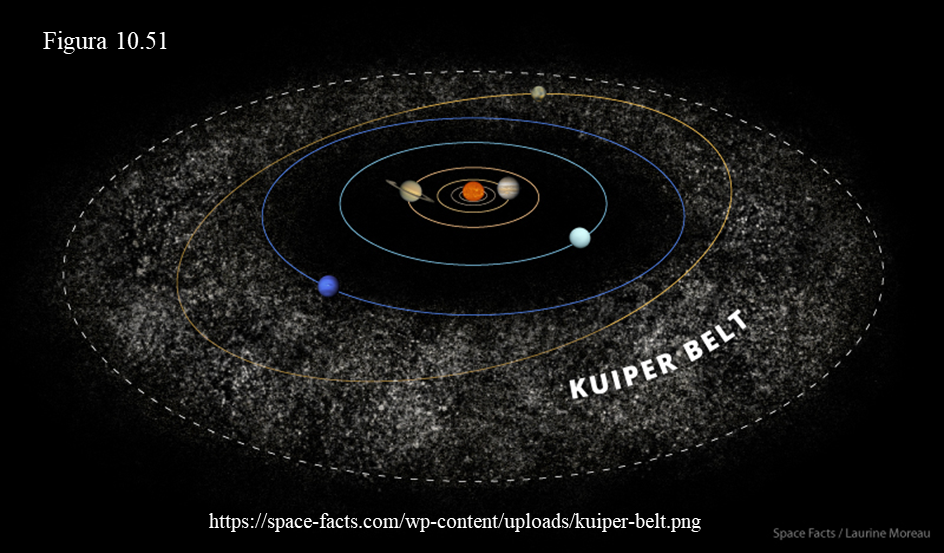
Los componentes del cinturón de Kuiper podrían darnos pistas sobre los primeros tiempos de la formación del sistema solar en estas zonas externas ya que parecen estar preservados tal y como se originaron (ver tema 11). Se les considera como un depósito de posibles cometas pues si sufren alguna perturbación gravitatoria podrían cambiar su órbita, “caer” hacia el interior del sistema y convertirse en un cometa de período corto o medio.
Finalmente, en la nube de Oort, una estructura esférica centrada en el Sol y que se extiende entre 1.000 y 100.000 UAs (¡más de un año luz!), están aparcados un gran número de objetos congelados que, si sufren alguna desestabilización en su órbita, pueden acercarse al centro y transformarse en un inesperado cometa, quizá visible desde nuestro planeta azul para nuestro asombro y admiración.
Ampliación: cálculo de masas
La Tierra
Cualquier objeto de cualquier masa m cae hacia la superficie terrestre con la misma aceleración (g = 9,8 m/s2). Esa aceleración se debe a la fuerza de atracción gravitatoria que la Tierra (de masa M) ejerce sobre él. Según la ley de la gravitación de Newton,
F = G·M·m / r2, siendo r la distancia entre el centro de la Tierra y el objeto, es decir, r = radio de la Tierra, pues suponemos que el objeto de masa m está muy próximo a la superficie terrestre.
La primera ley de la Mecánica nos dice que cualquier fuerza (F) va a provocar una aceleración (a) en el objeto de masa m, dada por F = m·a, en nuestro caso, F = m·g
Igualando F = G·M·m / r2 = m·g → M = g·r2 / G
G = 6,67·10-11 r = 6.371 km = 6,371·106 m g = 9,8 m/s2
MTierra = 9,8 · (6,371·106)2 / 6,67·10-11 = 6·1024 kg
Ejercicio 10.7
Para la Luna también es posible aplicar el mismo procedimiento, puesto que los astronautas que viajaron a nuestro satélite pudieron medir la aceleración de la gravedad allí: g = 1,625 m/s2.
Ahora M es la masa de la Luna, m es la del objeto que se deja caer sobre su superficie y el radio es r = 1.738 km = 1,738·106 m
- Calcula la masa de la Luna
- ¿Cuántas veces es mayor la masa de la Tierra que la de la Luna?
Haz clic aquí para ver la solución.
Júpiter
Un satélite orbita alrededor de su planeta debido también a la fuerza de atracción gravitatoria
F = G · M · m / r2, donde M es la masa del planeta, m la del satélite y r es la distancia entre ambos (o sea el radio de la órbita del satélite). El tirón gravitatorio del planeta hace que la trayectoria del satélite se curve continuamente de forma que describe una elipse, generalmente casi una circunferencia.
Y la aceleración centrípeta en un movimiento circular y uniforme viene dada por la fórmula
a = m·v2 / r siendo v la velocidad lineal del satélite. La fuerza que provoca esa aceleración centrípeta es, de nuevo, F = m·a
Igualando ambas fuerzas: G· M·m / r2 = m·v2 / r
Las masas m del satélite se pueden cancelar y podemos despejar M, la masa del planeta:
M = v2·r / G
v = velocidad lineal = 2·π·r / T siendo T el periodo del satélite medido en segundos.
Así que, M = (2·π·r / T)2 · r / G = 4·π2·r3 / (T2·G)
Para Io, los datos son estos:
Radio de su órbita r = 421.600 km = 4,216·108 m
Periodo T = 1,77 días = 1,77·24·60·60 = 152.928 s = 1,53·105 s
Resulta MJúpiter = 4·π2 · (4,21·108)3 / ( (1,53·105)2 ·6,67·10-11) = 1,9 · 1027 kg
Que es unas 317 veces la masa terrestre.
Ejercicio 10.8
El mismo procedimiento puede utilizarse con un planeta y su estrella central, siempre que la masa del planeta sea mucho más pequeña que la de la estrella y que su órbita sea prácticamente circular. Este es el caso del Sol y la Tierra.
Otra vez igualando la fuerza de atracción gravitatoria del Sol con la fuerza centrípeta que hace a la Tierra describir su órbita, resulta que G · M · m / r2 = m·v2 / r
M = masa del Sol, m la de la Tierra, r radio de la órbita de la Tierra (distancia media de la Tierra al Sol).
Como antes, las masas m del planeta se cancelan y
M = v2 · r / G → M = (2·π·r / T)2 · r / G = 4·π2·r3 / (T2·G)
Ahora r = 150·106 km = 1,5 · 1011 m
T = 365,25 días = 365,25 · 24 · 60 · 60 s = 3,156 · 107 s
- Calcula la masa del Sol.
- ¿Cuántas veces mayor es la masa del Sol en comparación con la de la Tierra?
Haz clic aquí para ver la solución.