- Portada
- Presentación
- Tema 1. Geografía celeste
- Tema 2. Movimiento de rotación
- Tema 3. Coordenadas ecuatoriales
- Tema 4. El modelo de las dos esferas
- Tema 5. La Luna
- Tema 6. Las 4 estaciones
- Tema 7. Relojes de Sol
- Tema 8. Calendarios y eclipses
- Tema 9. Los Planetas. Cinemática
- Tema 10. El Sistema Solar.
- Tema 11. La Tierra y la vida
- Tema 12. Prismáticos y telescopios
- Tema 13. Una noche de observación
- Tema 14. Distancia a las estrellas
- Tema 15. Vida y muerte de las estrellas
- Tema 16. La Vía Láctea
- Tema 17. Galaxias
- Tema 18. Cosmología
- Anexo. Grandes astrónomos
- Bibliografía y Webs
14.1 El método del paralaje
Si extendemos un brazo y levantamos el pulgar, al guiñar alternativamente un ojo u otro veremos cómo nuestro pulgar parece desplazarse respecto al fondo de la habitación. Quizá guiñando el ojo derecho veamos el pulgar justo delante de una esquina de la puerta, pero al guiñar el izquierdo lo veremos ligeramente desplazado. Este efecto de perspectiva se conoce con el nombre de paralaje y también puede observarse en las estrellas. Como la Tierra gira alrededor del Sol en un año, nuestra posición, nuestro «ojo», no tiene una posición fija. El 1 de enero y el 1 de julio (seis meses después) la Tierra ocupa posiciones diametralmente opuestas en su órbita (figura 14.1)
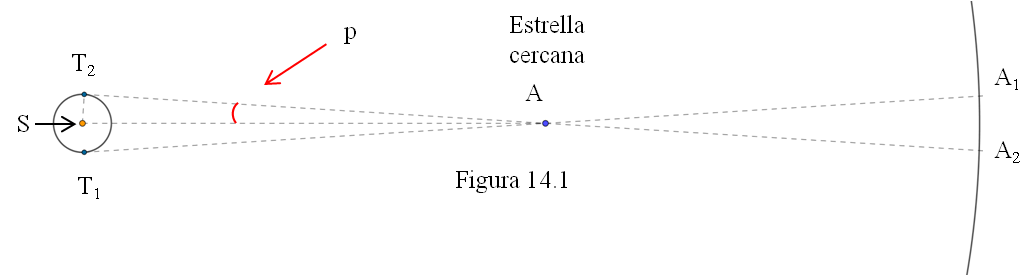
En esas dos fechas, una estrella cercana (A) se verá en posiciones diferentes con respecto al telón de fondo de las estrellas y constelaciones más alejadas. Mediante procedimientos complicados, los astrónomos han conseguido calcular el ángulo p (llamado paralaje de esa estrella); p es el ángulo con el que se vería el radio de la órbita terrestre desde esa estrella.
Como la distancia a las estrellas es enorme, estos ángulos, según se aprecia en la tabla siguiente, son siempre muy pequeños, del orden de fracciones de 1 segundo de arco, es decir, pequeñísimos. Hasta que los telescopios no fueron suficientemente potentes no se logró medir el paralaje de ninguna estrella. La primera vez que se consiguió fue en 1838, cuando el astrónomo alemán Friedrich Bessel consiguió medir el de la estrella 61 Cygni. Pero lo que nos importa es que ese ángulo sólo depende de la distancia, y viceversa: conociendo ese ángulo podemos calcular la distancia.
La unidad habitual para medir las distancias astronómicas es el año luz: la distancia que recorre la luz en un año. Para simplificar los cálculos, los astrónomos han ideado una nueva unidad de distancias: el parsec (pc). 1 parsec (abreviatura de paralaje segundo) es la distancia a la que tiene que estar una estrella para que su ángulo de paralaje sea p = 1″. La equivalencia entre ambas unidades es 1 pc = 3,26 años luz.
Ampliación: cálculo trigonométrico de distancias por paralaje
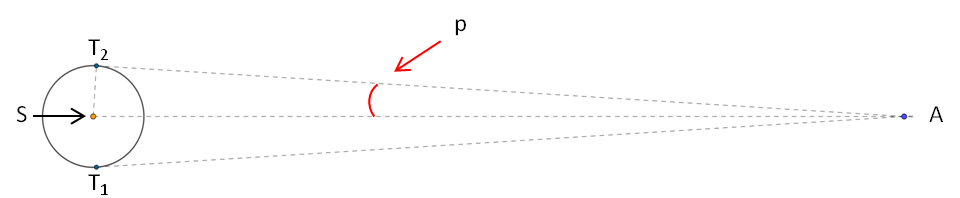
La línea AT2 es tangente a la órbita terrestre por lo que también es perpendicular al radio ST2 y el triángulo ST2A es un triángulo rectángulo (T2 = 90º).
Por tanto sen p = ST2/SA
Si p = 1” → sen 1” = 150·106 km / SA → SA = 150·106 km/sen 1”
SA = 1 pc (por definición) = 150·106 km/0,00000485 = 3,09·1013 km (¡casi 31·1012de km!)
Como 1 año luz = 300.000·60·60·24·365 = 9,46·1012 km
Resulta que 1 pc = 3,09·1013 km/9,46·1012 km = 3,26 años luz
En esta tabla aparece el nombre de la estrella, su paralaje (p, en segundos de arco), su distancia (en parsecs) y su distancia (en años luz). Los huecos en los nombres de las estrellas quieren decir que no hay ninguna que esté exactamente a esa distancia.
Tabla de paralajes y distancias
| Estrella | p (”) | Distancia | Estrella | p (”) | Distancia | |||
| pc | a.l. | pc | a.l. | |||||
| 1 | 1 | 3,26 | 0,1 = 1/10 | 10=1/0,1 | ||||
| α Centauri | 0,77 | Capella | 0,07 | |||||
| 0,5=1/2 | 2=1/0,5 | Aldebarán | 0,05 | |||||
| Sirio | 0,37 | Achernar | 0,028 | |||||
| Proción | 0,29 | Spica | 0,013 | |||||
| 0,25=1/4 | 4=1/0,25 | 0,01=1/100 | 100=1/0,01 | |||||
| Altair | 0,2 | Betelgeuse | 0,006 | |||||
| Vega | 0,12 | |||||||
Para estos ángulos tan pequeñísimos sí que se da una proporcionalidad precisa: si el ángulo es la mitad (p = 1/2 = 0,5”) entonces la distancia tiene que ser justo el doble, para p = 1/3 = 0,333…” la estrella estará el triple de lejana, etc.
Ejercicio 14.1
a) Completa la tercera columna (la correspondiente a las distancias en parsecs).
b) Completa ahora (es más fácil) la última columna, las distancias en años luz. Recuerda que 1 parsec = 3,26 años luz.
Haz clic aquí para ver la solución.
La medida de ángulos tan pequeños es muy difícil y los instrumentos y telescopios terrestres sólo permitían calcular con precisión las distancias, por el procedimiento del paralaje, hasta un límite máximo de unos 100 parsecs. Recientemente se ha producido un avance espectacular con la utilización de sondas espaciales (Hipparcos, Gaia, ambas de la Agencia Espacial Europea) en órbita más allá de la molesta atmósfera terrestre. La misión Gaia está permitiendo medir distancias por paralaje hasta unos 30.000 años luz de distancia.
Pero hay estrellas y galaxias mucho más lejos todavía cuya distancia sigue siendo imposible de medir por este procedimiento. La inventiva humana tuvo que buscar otros procedimientos, y encontró muchos más. Algunos de los más importantes son los que se describen a continuación.