Algunas estrellas no tienen un brillo fijo y constante, sino que a veces parecen brillar más y a veces menos. Se llaman, muy adecuadamente, estrellas variables. Una de las más conocidas es Algol (β Persei), que oscila periódicamente entre la 2ª y la 3ª magnitud en unos tres días. Otra famosa estrella variable es Mira (en la constelación de Cetus, la Ballena) que desciende desde la 2ª magnitud ¡hasta la 10ª!, pero muy despacio, en algo menos de un año.

Las estrellas variables se clasifican en diversos grupos, en función de cuál sea la causa de su variación. El grupo más interesante para el cálculo de distancias es el de las variables cefeidas, llamadas así porque su estrella tipo es la δ de la constelación de Cefeo, situada muy cerca de la esquina de esta constelación que está más lejos de la Polar (figura 14.5).

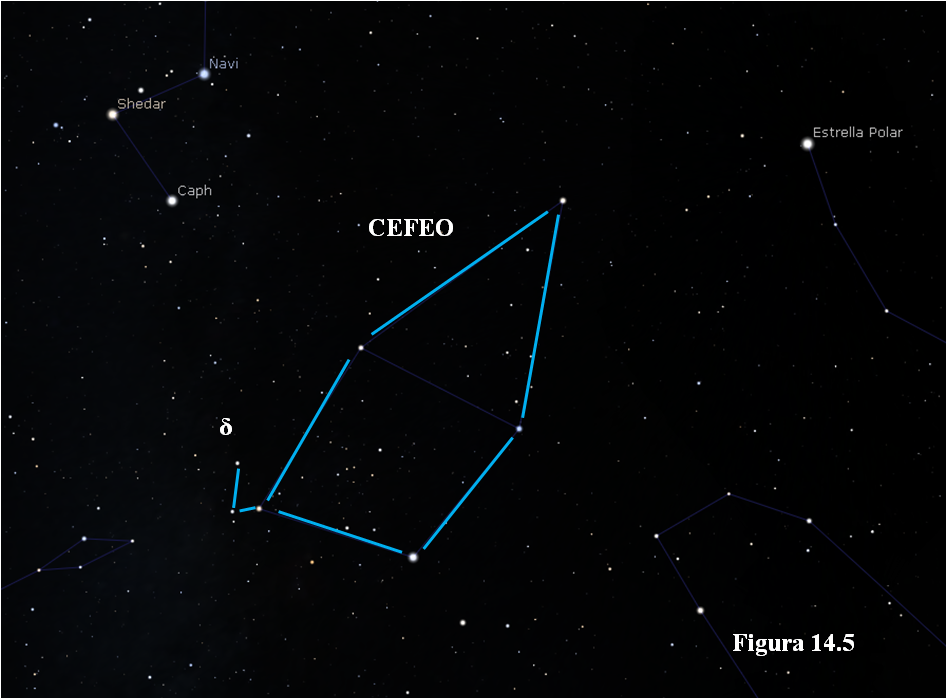
Todas las cefeidas tienen un brillo variable que oscila entre un mínimo y un máximo en unos cuantos días. En la lección 15 se explica la causa de esta variación. Si se confecciona una gráfica situando en el eje OX el tiempo, en días, y en el eje OY la magnitud aparente, se obtiene la curva de luz de esa estrella.

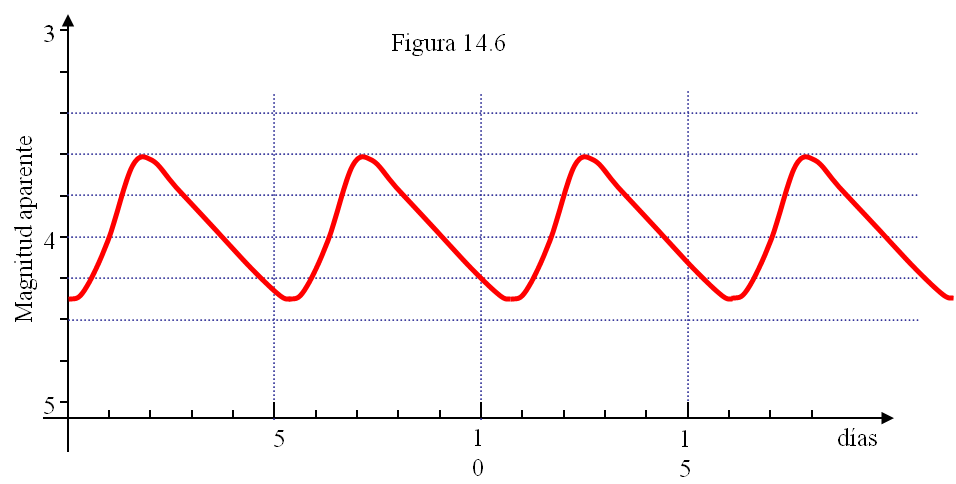
En la figura 14.6 aparece la curva de luz de δ Cephei. La distancia entre un mínimo y el siguiente (o entre un máximo y el siguiente) es el período de esa estrella.

Ejercicio 14.5

Observando la curva de luz de δ Cephei, averigua cuál es su período. ¿Cuál es su magnitud en el máximo de su brillo? ¿Y su magnitud en el mínimo? ¿Cuál es su magnitud media?

Haz clic aquí para ver la solución

En Astronomía, como en cualquier otra ciencia, es necesario recoger y organizar gran cantidad de datos para estudiar si podemos obtener de ellos alguna información interesante, para intentar reconocer pautas, regularidades y coincidencias que permitan obtener leyes y fórmulas que nos ayuden a comprender cómo funciona la Naturaleza. Esto fue lo que hizo, a principios del siglo XX, la norteamericana Henrietta S. Leawit, quien descubrió así una ley que ha resultado ser fundamental para el cálculo de distancias en el Universo. La siguiente actividad reproduce, muy simplificadamente, sus investigaciones.

Ejercicio 14.6

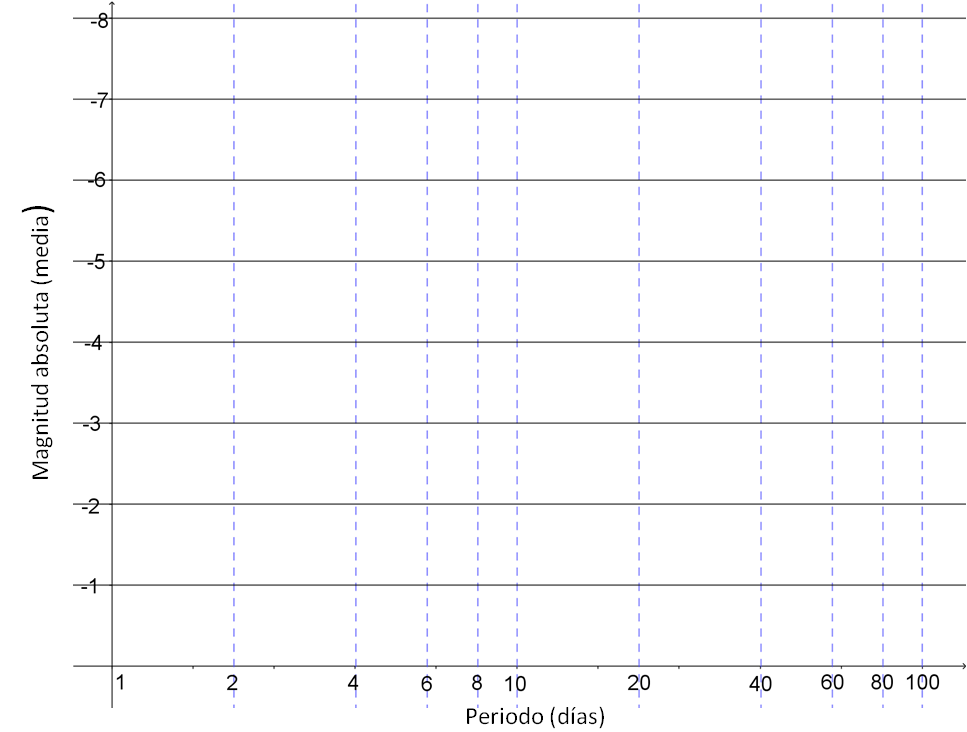
En la tabla inferior se recogen los datos (período y magnitud absoluta media) de cinco cefeidas. En la figura hay unos ejes de coordenadas. El horizontal corresponde al tiempo (en días, con escala logarítmica) y el vertical a la magnitud absoluta media.

a) Señala un punto para cada una de las estrellas de la tabla.

b) Posteriormente une los cinco puntos obtenidos mediante una línea.

Periodo (días)	5,4	10	22,4	31,6	79,4
M absoluta (media)	– 3,4	– 4	– 4,9	– 5,3	– 6,2

Haz clic aquí para imprimar la gráfica

Haz clic aquí para ver la solución

Ejercicio 14.7

Para resolver este ejercicio necesitas la solución del anterior. Consúltala si fuera necesario.

Si observando una cefeida llegamos a la conclusión de que su período es de 50 días, ¿puedes averiguar, con ayuda de esa línea que acabas de trazar en la figura del ejercicio anterior, cuál es su magnitud absoluta media?, ¿y para una cefeida cuyo período es de 15 días?

Haz clic aquí para ver la solución

En realidad lo que observó Henrietta S. Leavitt fue una relación entre el periodo y la magnitud aparente de 25 cefeidas situadas en la Pequeña Nube de Magallanes. Pero al estar todas ellas dentro de dicha nube, supuso correctamente que sus distancias eran aproximadamente iguales y dedujo que la relación descubierta era entre el periodo y la magnitud absoluta.

Para poder utilizar este hecho en otras regiones del cielo hacía falta calibrar esa relación encontrando (por paralaje) las distancias a algunas cefeidas próximas para poder así calcular su magnitud absoluta y obtener la formulación final que relaciona el periodo con la magnitud absoluta. El primero en hacerlo fue Ejnar Herzsprung (uno de los creadores del diagrama HR, ver lección 15) y posteriormente ha sido verificada y ajustada con buena precisión.

Así que, a partir del período de una cefeida podemos deducir cuál es su magnitud absoluta media. El período se puede averiguar observando esa estrella de manera continua y trazando su curva de luz. Por tanto no es muy difícil hacerlo y llegar a conocer la magnitud absoluta de esa estrella. Pero su observación también nos permite saber cuál es su magnitud aparente. Y si sabemos la magnitud absoluta y la aparente podremos, ¡por fin!, hallar la distancia a la que está esa estrella. Esto es lo que vas a hacer a continuación.

Ejercicio 14.8

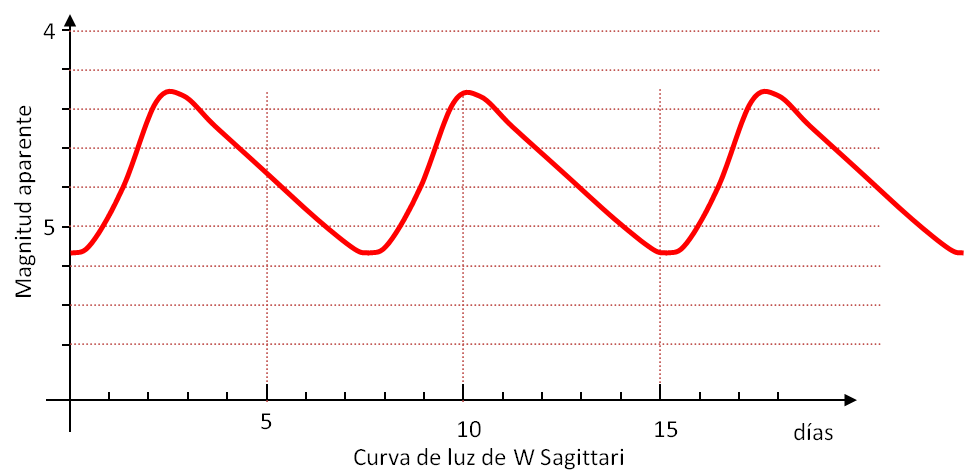
La figura inferior muestra la curva de luz de otra cefeida, la W de la constelación de Sagitario (W Sagittari). A partir de esta curva de luz calcula:

1. La magnitud aparente media de W Sagittari
2. Su período en días.
3. Conocido su período y utilizando la tabla del ejercicio 14.6, determina su magnitud absoluta media.
4. Conocidas sus magnitudes medias aparente y absoluta, y con ayuda de la figura 14.3, averigua la distancia de W Sagittari a la Tierra.

Haz clic aquí para ver la solución

Como las cefeidas son muy luminosas este método para averiguar la distancia a una estrella se puede aplicar con éxito hasta una distancia de unos 100 millones de años luz, con lo que es posible detectarlas en galaxias no muy lejanas y determinar así su distancia (ver tema 18).