Curso General de Astronomía
Tema 15. Vida y muerte de las estrellas
KEPLER. GRUPO DOCENTE DE ASTRONOMÍA
- Portada
- Presentación
- Tema 1. Geografía celeste
- Tema 2. Movimiento de rotación
- Tema 3. Coordenadas ecuatoriales
- Tema 4. El modelo de las dos esferas
- Tema 5. La Luna
- Tema 6. Las 4 estaciones
- Tema 7. Relojes de Sol
- Tema 8. Calendarios y eclipses
- Tema 9. Los Planetas. Cinemática
- Tema 10. El Sistema Solar.
- Tema 11. La Tierra y la vida
- Tema 12. Prismáticos y telescopios
- Tema 13. Una noche de observación
- Tema 14. Distancia a las estrellas
- Tema 15. Vida y muerte de las estrellas
- Tema 16. La Vía Láctea
- Tema 17. Galaxias
- Tema 18. Cosmología
- Anexo. Grandes astrónomos
- Bibliografía y Webs
15.1 Características estelares
Denominación
Como hemos ido viendo a lo largo del curso, las estrellas más brillantes del cielo tienen nombres propios que hacen referencia a la mitología griega, árabe, etc. Como Sirio, Rígel, Proción, Deneb, Aldebarán…, pero la mayor parte de ellas de menor luminosidad no tienen nombre propio. En 1603 J. Bayer, un abogado de Augsburgo, introdujo una denominación metódica. Dentro de cada constelación, las estrellas se nombran en función de su brillo siguiendo las letras del alfabeto griego (α, β, γ, δ, ε…) y a continuación el genitivo latino de la constelación. Por ejemplo Régulus, la estrella más brillante de la constelación de Leo, se denomina como α Leonis, la segunda en brillo (Denébola) se designa como β Leonis, la tercera (Algieba) es γ Leonis, etc. A menudo se utiliza solo la abreviatura de la constelación (α Leo). Cuando no basta el alfabeto griego se utiliza el alfabeto latino e incluso números; por ejemplo, la primera estrella en la que fue descubierto un exoplaneta es 61 Pegasii. Como excepción a esta regla está la constelación de la Osa Mayor (figura 15.1), cuyas estrellas de brillo parecido se denominan según la posición que ocupan, así Dubhe es α Ursa Majoris, Merak es β Ursa Majoris, Phecda corresponde a γ Ursa Majoris,…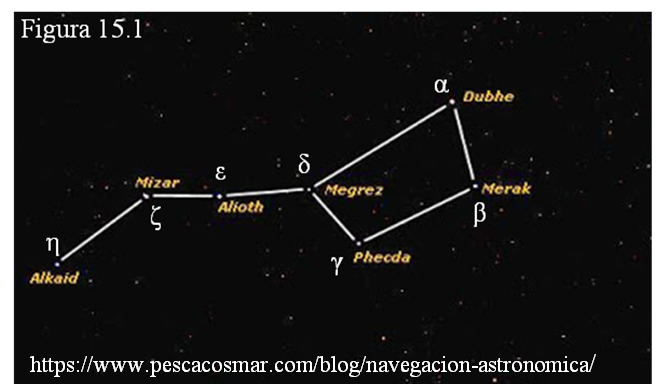
Brillo de una estrella
Para el ojo humano, una estrella es sólo un punto luminoso. En realidad cada estrella es un Sol, algo semejante al nuestro. Es también una fantástica reserva de energía nuclear. Lo primero que llama la atención al mirar al cielo en una noche oscura es la gran variedad de luminosidad que presentan las estrellas. Algunas de ellas son tan débiles que el ojo humano no las puede detectar, mientras que otras poseen un brillo intenso comparable a los planetas. A simple vista y en un muy buen lugar de observación podemos observar de 2.500 a 3.000 estrellas. En el tema anterior tratamos de la magnitud aparente. Se observó que había estrellas y planetas cuyo brillo era más intenso que el correspondiente a primera magnitud. Se recurrió a magnitudes 0, -1, -2, -3, etc. Con las nuevas técnicas e instrumentos es posible medir con más precisión el brillo aparente de los astros y adjudicarles una magnitud aparente con decimales. La estrella más brillante, Sirio, tiene un magnitud de -1,5 y Venus puede alcanzar la magnitud de -4,4; la Luna llena alcanza magnitud de -12,7 y el Sol -26,8. Los grandes telescopios terrestres pueden identificar objetos tan tenues como de magnitud 24. La tabla siguiente presenta las estrellas más brillantes visibles desde nuestra latitud| Nombre | Constelación | Brillo | Distancia (Años-luz a.l.) | |
| 1 | Sirio | Can mayor | -1,44 | 8,6 |
| 2 | Arturo | Boyero | -0,05 | 36 |
| 3 | Vega | Lira | 0,03 | 26 |
| 4 | Capella | Auriga | 0,08 | 42 |
| 5 | Rígel | Orión | 0,18 | 900 |
| 6 | Proción | Can menor | 0,40 | 11,3 |
| 7 | Achernar | Eridano | 0,45 | 140 |
| 8 | Betelgeuse | Orión | 0,45 | 310 |
| 9 | Altair | Águila | 0,76 | 16 |
| 10 | Aldebarán | Toro | 0,87 | 68 |
| 11 | Spica | Virgo | 0,98 | 260 |
| 12 | Antares | Escorpio | 1,06 | 600 |
| 13 | Pollux | Géminis | 1,16 | 34 |
| 14 | Fomalhaut | Pez Austral | 1,17 | 25 |
| 15 | Deneb | Cisne | 1,18 | 3.200 |
| 16 | Regulus | Leo | 1,25 | 77 |
Tamaño, masa
Aún con los más potentes telescopios la imagen de las estrellas se reduce a un mero punto. Sólo en casos excepcionales, estrellas enormemente grandes y relativamente próximas como Betelgeuse o Antares (figura 15.2, se ha conseguido detectarlas como un círculo de cierto tamaño aparente lo que ha permitido medir su radio conociendo su distancia. En general el tamaño de una estrella se calcula a partir de su magnitud absoluta y su temperatura superficial mediante la ley de Stefan – Boltzman (ver la ampliación).

Una de las estrellas conocidas más grandes es VY Canis Majoriscuyo diámetro es unos 1.420 el diámetro del Sol, que englobaría hasta la ór-bita de Urano. Entre las estrellas más pequeñas están las enanas blancas del tamaño de la Luna o las estrellas de neutrones, que pueden reducir su tamaño hasta unos 20 km.La tabla inferior muestra el tamaño de algunas estrellas conoci-das(figura 15.3)
| Estrella | Constelación | Diámetro | Estrella | Constelación | Diámetro | |
| VY Canis Majoris | Can Mayor | 1.420 | Deneb | Cisne | 200 | |
| Arturo | Boyero | 25 | ||||
| Betelgeuse | Orión | 900 | Vega | Lira | 2,5 | |
| Antares | Escorpión | 750 | Altair | Águila | 1,8 |
A diferencia del diámetro, las estrellas varían en masa relativamente poco, las estrellas más masivas poseen una masa unas 1.000 veces superior a las más ligeras, una estrella supermasiva como HD 698 contiene unas 113 masas solares.

Ampliación: el tamaño de las estrellas
El tamaño (el radio R) de las estrellas se calcula teóricamente conociendo su luminosidad L y su temperatura T utilizando esta fórmula: L = 4·π·R2·σ·T4
σ es la constante de Stefan-Boltzman σ = 5.67·10-8 Wm-2K-4
Esta ley nos dice que la luminosidad depende de la T superficial de la estrella y de su tamaño, de su superficie: 4·π·R2.
En la práctica es más fácil calcular el radio de la estrella en términos del radio solar.
Para el Sol, también LS = 4·π·R2·σ·T4
Dividiendo, las constantes se eliminan y nos queda L/LS = (R/RS)2·(T/TS)4
La proporción L/LS se puede calcular sabiendo la magnitud absoluta M de esa estrella y la del Sol MS = 4,83
Por ejemplo, Sirio tiene una M = 1,44. Por tanto es más luminosa que el Sol, ¿cuánto?
La diferencia de magnitudes absolutas es ΔM = 3,39, por lo que la luminosidad de Sirio será:
2,5123,39 = 22,7 veces la del Sol: L/LS = 22,7
La temperatura T de una estrella se puede conocer a través de su clasificación espectral.
Sirio es una estrella A1 por lo que su T = 9.700 K
Así que T/TS = 9.700 / 5.800 = 1,67 y (T/TS)4 = 7,823
Sustituyendo 22,7 = (R/RS)2·7,823
Obtenemos (R/RS)2 = 22,7/7,823 = 2,9
Por tanto R/RS = 2,91/2 = 1,7
El radio de Sirio es 1,7 veces el solar
Ampliación: la masa de las estrellas
En una estrella binaria, formada por dos (A y B) muy próximas, las leyes de la gravedad las obligan a un baile conjunto. Cada una de ellas describe una órbita elíptica alrededor del centro de masas común (G) de forma que la recta que une A y B tienen que pasar por G que no está en el centro del segmento AB sino más cerca de la estrella más masiva (A) de forma que se cumpla la ley de la palanca:
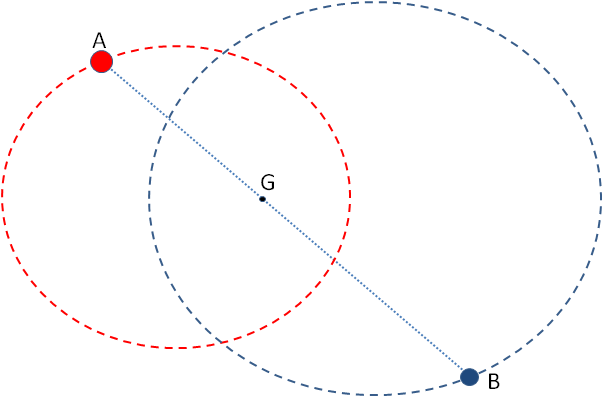 GA·MA = GB·MB (como un balancín).
GA·MA = GB·MB (como un balancín).
En esta figura, MA = 1,3·MB con lo que en todo momento GB = 1,3·GA. Las dos elipses tienen que tener la misma excentricidad (la misma forma, aunque la que describe B es 1,3 veces mayor que la de A) y G es uno de los focos en ambas órbitas.
Desde la Tierra es más fácil observar el movimiento aparente de la menos masiva (B) con respecto a A.
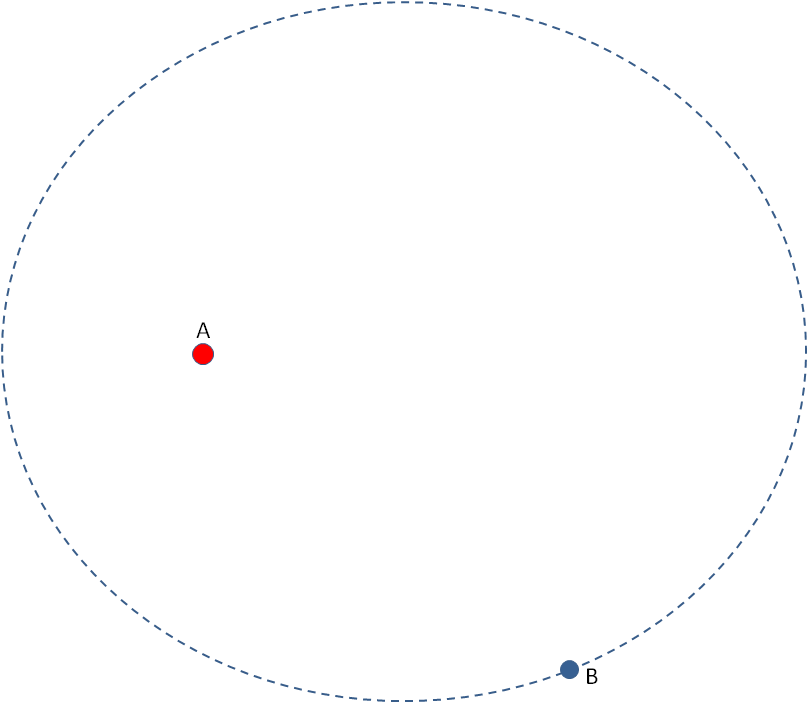 El resultado es también una elipse con la misma excentricidad. Por observación directa es posible determinar el periodo P que B tarda en completar su recorrido, así como la amplitud visual de esa elipse, el ángulo que ocupa su eje mayor.
El resultado es también una elipse con la misma excentricidad. Por observación directa es posible determinar el periodo P que B tarda en completar su recorrido, así como la amplitud visual de esa elipse, el ángulo que ocupa su eje mayor.
En estas condiciones la tercera ley de Kepler permite calcular sus masas:
MA + MB = a3/P2
donde a es el semieje de la elipse aparente de B alrededor de A expresado en UA (unidades astronómicas) y P es el periodo, el tiempo que se tarda en completar una órbita, expresado en años. El resultado se obtendrá en masas solares.
Si, además, es posible determinar la relación de distancias al centro de gravedad común, entonces también conoceremos la relación entre sus masas MA/MB.
Por ejemplo, la estrella binaria 70 Ophiuchi, tiene un periodo P = 88,4 años, está a una distancia de 5 pc y el semieje mayor de la órbita aparente de 70 Ophiuchi B alrededor de su compañera 70 Ophiuchi A se ve con un ángulo de 4,66”.

Ya lo tenemos casi todo. Nos falta obtener la longitud del semieje mayor (a) en UA. A una distancia de 1 pc un ángulo de 1” abarcará exactamente 1 UA (esto por definición de pc). Por tanto a 5 pc, un ángulo de 1” abarcará 5 UA.

Como para estos ángulos tan minúsculos se mantiene la proporcionalidad (tema 14, paralaje) podemos asegurar que un ángulo de 4,66” abarcará una distancia de 5·4,66 = 23,3 UA, que es lo que mide el semieje (a). Por tanto
MA + MB = a3/P2 = 23,33/88,42 = 1,6·MS
Pero también se ha podido averiguar que la distancia del centro de gravedad común (G) a la estrella menor (B) es siempre GB = 1,25 GA
Eso quiere decir que MA = 1,25·MB
Por lo tanto MA + MB = 1,25·MB + MB = 2,25·MB = 1,6·MS
MB = 1,6/2,25 MS = 0,71·MS
MA = (1,6 – 0,71)·MS = 0,89·MS
Color y espectro
Cuando calentamos un alfiler con una llama, va cambiando de color según sea su temperatura: primero adquiere el color rojo, después anaranjado, a continuación amarillo y finalmente blanco. Es decir, el color de los cuerpos depende de su temperatura. Las estrellas también presentan diversos colores que están en función de su temperatura superficial.
Si se hace pasar un rayo de luz solar a través de un prisma aparece el arco iris, formado por una gama de colores que varían gradualmente desde el violeta, en un extremo, hasta el rojo, en el otro. Así se descubrió que la luz blanca consistía en la mezcla de varios colores. También se descubrió que más allá del violeta llegaban otros tipos de rayos, los cuales calentaban mucho un termómetro, pero eran invisibles. Y lo mismo ocurre más lejos del extremo rojo del arco iris.

La luz está formada por muchos rayos diferentes, unos visibles con diferentes colores y otros invisibles. Todos ellos son ondas electromagnéticas que viajan a la misma velocidad, la velocidad de la luz c = 300.000 km/s. Pero cada color o cada tipo de radiación posee diferente longitud de onda. Una onda electromagnética puede entenderse como una vibración, como una curva que oscila continuamente produciendo crestas y valles. La distancia entre dos crestas sucesivas (o entre dos valles sucesivos) es lo que se llama longitud de onda (λ). Esta distancia es la que distingue un color de otro y un tipo de radiación de otra.

Las longitudes de onda suelen ser muy pequeñas y para medirlas se utiliza el nanómetro (nm). 1 nm = 10-9 m. Así, la luz roja tiene una λ = 750 nm mientras que la λ de la luz violeta es de 400 nm. Los famosos rayos ultravioletas tienen una λ aún más pequeña y ya no son visibles. La radiación infrarroja, por el contrario, tiene una λ mayor de 750 nm y nuestros ojos tampoco son capaces de detectarla, como ocurre con los rayos X, utilizados en las radiografías, las microondas o las ondas de radio y de televisión.
El espectro electromagnético es el conjunto de todas estas ondas. La figura 15.6 representa todo el espectro en función de la longitud de onda λ

En 1812 el óptico alemán Fraunhofer hizo pasar la luz del Sol, primero a través de una rendija muy estrecha, y después, a través de un prisma. Observó que sobre el fondo del arco iris aparecían muchas rayas oscuras, cada una situada en una posición determinada por su longitud de onda. Esta serie de líneas superpuestas al fondo del arco iris es lo que se llama el espectro de la luz solar.
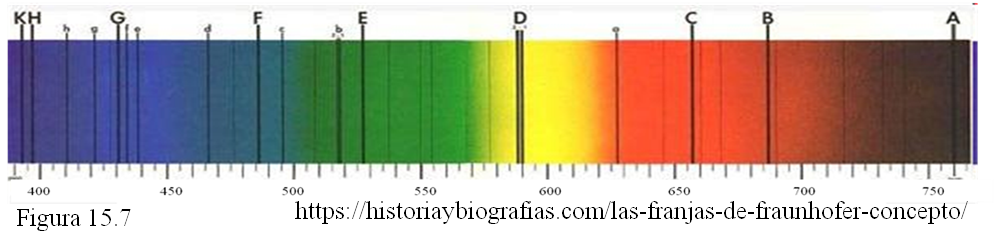
A lo largo del siglo XIX se descubrió que cada elemento químico produce en el espectro unas rayas oscuras determinadas y específicas: el hidrógeno, por ejemplo, siempre produce una raya en 434 nm, otra en 486 nm (la F en la figura 15.7) y otra con λ = 656 nm (la C). Es algo parecido a los códigos de barras de las etiquetas de muchos productos, los cuales permiten identificar de qué producto se trata, cuál es su precio y otros datos del mismo. Las rayas oscuras en el espectro son como las huellas dactilares de cada elemento químico. Gracias a ellas se pudo identificar la mayoría de las líneas oscuras de Fraunhofer en el espectro de la luz solar y fue posible averiguar cuál es la composición química del Sol.
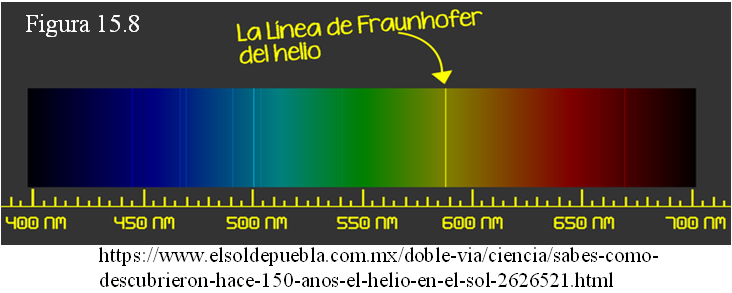
En 1868 el astrónomo francés Pierre Janssen observó en el espectro solar algunas líneas oscuras que no se correspondían con las de ningún elemento conocido. Al mismo tiempo el inglés Norman Lockyer había logrado un descubrimiento similar. Se bautizó este nuevo elemento (que parecía ser exclusivo del Sol) como “Helio”, en honor al nombre del dios griego del Sol. Hubo que esperar hasta 1882 cuando el físico italiano Luigi Palmieri descubriría la presencia de este elemento en la atmósfera terrestre.
Clasificación espectral

El paso siguiente fue intentar analizar la luz de las estrellas. El instrumento necesario para hacerlo se llama espectroscopio (figura 15.9). Acoplado a un telescopio, permite obtener el espectro de cualquier estrella, siempre que sea suficientemente brillante. Así pudieron emprenderse estudios sobre la composición química y sobre el estado físico de las estrellas, hasta entonces inabordables. Se produjo un vuelco, y los cálculos de posiciones y movimientos quedaron relegados a segundo plano, mientras una nueva ciencia se situaba en el primer puesto del interés: la Astrofísica.
El espectro de las estrellas es prácticamente nuestra única fuente de información sobre ellas. Afortunadamente es impresionante la cantidad de datos que se puede extraer de su análisis. Uno de ellos es la temperatura superficial de la estrella.
Las estrellas emiten luz de todos los colores, cuya mezcla hace que las veamos blancas. Sin embargo, en muchas es posible apreciar ciertos tonos de colores, sobre todo los rojizos, como es el caso de Betelgeuse o de Antares. El Sol es claramente amarillento. Esto se debe a que nuestra estrella lanza al espacio más cantidad de radiación amarilla que de otras longitudes de onda.
Analizando el espectro de una estrella es posible determinar cuál es la longitud de onda (λmáx) en la que emite un máximo de radiación. Concretamente, la longitud de onda más intensa en la luz solar es λmáx = 500 nm. Esa longitud de onda está entre el verde y el azul. Sin embargo, el Sol emite en conjunto más radiación en el amarillo y por eso lo vemos de ese color. Y hay una ley física, la ley de Wien, que permite calcular la temperatura superficial de esa estrella:
T (K) = 2.900.000/λmáx (nm)
Para el Sol T = 2.900.000/500 = 5.800 K
Ejercicio 15.1
a) La λmáx de Arturo es de 676 nm. Este máximo, ¿está más cerca del extremo rojo o del extremo violeta de la luz visible? ¿De qué tono crees que será el color de Arturo?
b) Calcula, utilizando la fórmula de la ley de Wien, la temperatura superficial de Arturo.
c) Averigua el color y la temperatura de Vega (λmáx=302 nm).
Haz clic aquí para ver la solución
Hacia 1900 se habían recogido y fotografiado los espectros de muchas estrellas. En unos aparecían pocas rayas oscuras, en otros muchas. En todos había H y He pero en algunos también se identificaron ciertos metales como el sodio (Na), el calcio (Ca) o el magnesio (Mg). Tras muchos estudios, entre los que destaca la aportación de la norteamericana Annie J. Cannon del observatorio de Harvard en Boston, se estableció la siguiente clasificación de las estrellas según su espectro:
| Clase espectral | Estrella tipo | Color | Temperatura (K) |
| O | λ Cephei | Azul | > 30.000 |
| B | Spica | Blanco – Azul | 10.000 – 30.000 |
| A | Vega | Blanco | 7.500 – 10.000 |
| F | Procion | Blanco – Amarillo | 6.000 – 7.500 |
| G | Sol | Amarillo | 5.000 – 6.000 |
| K | Arturo | Naranja | 3.500 – 5.000 |
| M | Betelgeuse | Rojo | 2.000 – 3.500 |
La designación de cada clase espectral con una letra mayúscula es un mero convenio, y el orden en el que aparecen se debe a que inicialmente se hizo una clasificación provisional siguiendo el orden alfabético. Luego se encontró más lógico seguir el orden de temperaturas o de los colores. Los estudiantes de habla inglesa utilizan esta frase para recordar la secuencia de letras.
Oh!, Be A Fine Girl, Kiss Me
Una versión castellana, menos romántica, dice así:
«Otros Buenos Astrónomos Fueron Galileo, Kepler, Messier»
Cada clase espectral se subdivide en 10 partes, desde la 0 hasta la 9, para afinar más esta clasificación. Por ejemplo, una estrella G0 tendría la máxima temperatura (6.000 K), mientras que la G9 tendría una temperatura un poco mayor de 5.000 K. El Sol es de la clase G2.
Ejercicio 15.2
Indica la clase espectral a la que pertenece Capella, cuya temperatura superficial es de 5.900 K. Clasifica estas estrellas
a) Rigel (λmáx = 230 nm) b) Altair (T = 8.400 K) c) Aldebarán (T = 4.200 K).
Haz clic aquí para ver la solución
.