El desplazamiento al rojo

Ya se ha visto que uno de los principales recursos de los astrónomos es el espectro, ese arco iris surcado por múltiples rayas oscuras. Gracias al estudio de los espectros se han podido averiguar muchas cuestiones acerca de las estrellas. Ahora vamos a utilizarlos para estudiar la estructura del Universo a gran escala.

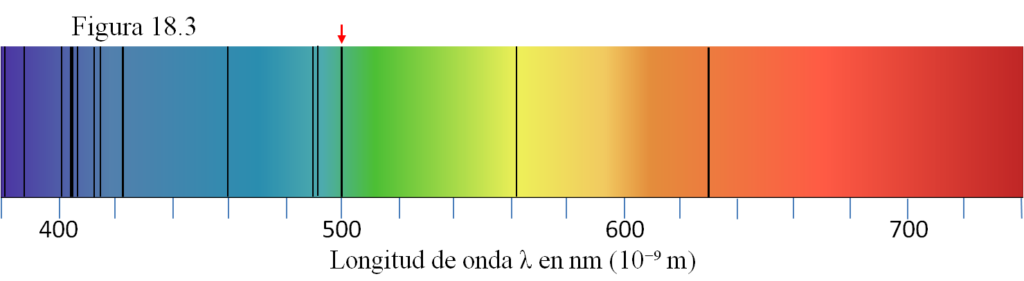
La figura 18.3 es un esquema muy simplificado del espectro ordinario de la luz solar, en el que sólo se han representado algunas rayas oscuras características. Una de ellas, la de 500 nanómetros (nm) de longitud de onda, se ha señalado con una flecha roja.

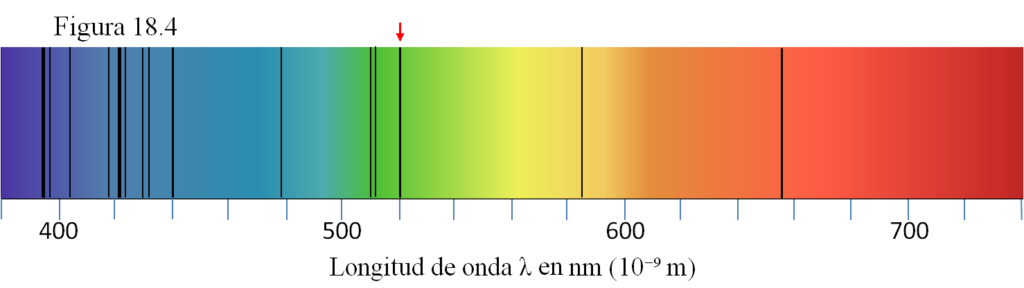
El espectro (figura 18.4, también esquematizado, como todos los que aparecerán en este tema) producido por una lejana galaxia es muy parecido al ordinario correspondiente al Sol: la secuencia de rayas oscuras es la misma. Pero hay una pequeña diferencia: todas las rayas están un poco desplazadas hacia la derecha, hacia el rojo. La línea que tenía una λ₀ = 500 nm ahora aparece con λ = 520 nm.

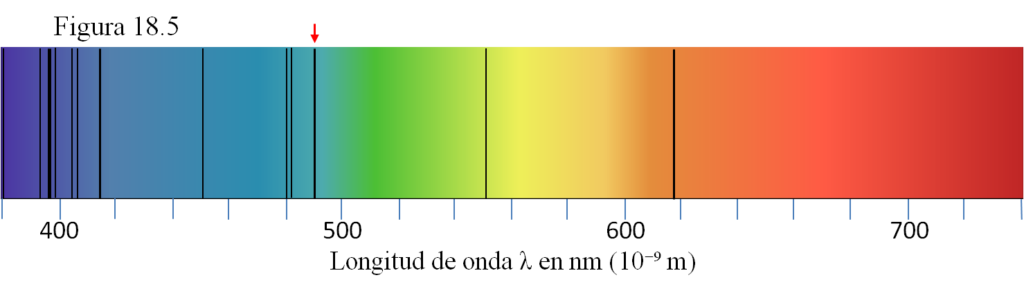
También hay objetos (estrellas, nebulosas o alguna galaxia, como Andrómeda) cuyo espectro presenta un desplazamiento hacia el azul (figura 18.5).

En astronomía siempre (aunque sea hacia el azul) se habla del desplazamiento al rojo (o redshift, de su nombre en inglés) que se cuantifica de esta manera: z = Δλ / λ₀ = (λ – λ₀)/λ₀

Por ejemplo, en la figura 18.4, λ₀ = 500, λ = 520 → Δλ = 20 → z = 20/500 = 0,04

En cambio en la figura 18.5, λ₀ = 500, λ = 490 →Δλ = -10→ z = -10/500 = – 0,02

Ejercicio 18.1

Calcula el valor de z en estos tres espectros:

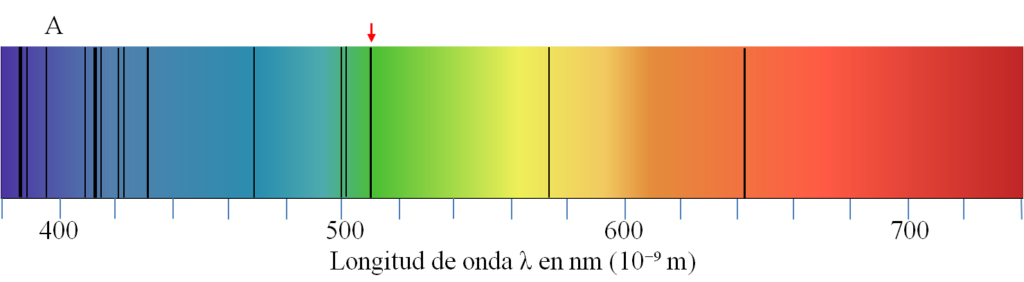
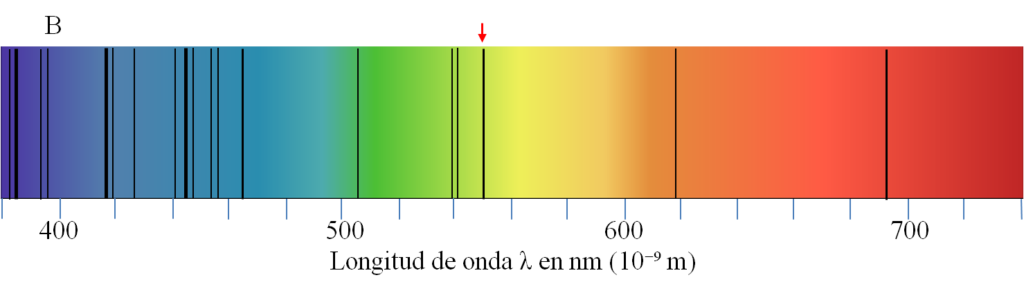
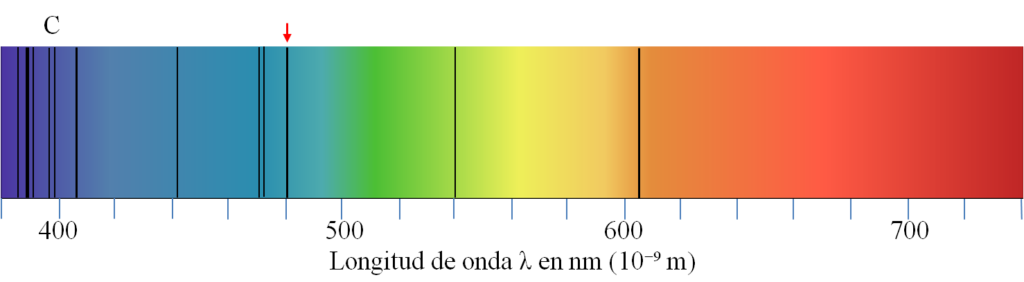
Haz clic aquí para ver la solución.

El valor de z indica en qué fracción la longitud de onda inicial λ₀ ha variado y es equivalente al porcentaje: un valor de z = 0,02 nos viene a decir que λ₀ se ha ampliado en un 2%. Y si tuviéramos z = 0,15 es que la longitud de onda ha aumentado un 15%.

El efecto Doppler

La primera interpretación de esos desplazamientos de las rayas espectrales daban por supuesto que el objeto emisor en cuestión está en movimiento respecto a nosotros. Es lo que se conoce como el efecto Doppler: siempre que una fuente de luz se aleje del observador, éste verá las rayas oscuras desplazadas hacia el rojo. Y, al revés, si la fuente de luz se acerca al observador las rayas se desplazarán hacia la izquierda, hacia el violeta, apareciendo las líneas espectrales con una λ algo menor (figura 18.4).

Lo mismo sucede con las ondas sonoras. Todos hemos tenido esta experiencia: si una ambulancia se está acercando velozmente hacia nosotros las ondas que emite las recibimos con una menor longitud de onda (y por tanto con una frecuencia mayor) y oiremos su sirena con un tono más agudo. En cambio, cuando ya haya pasado y se aleje recibiremos su señal desplazada hacia longitudes de onda mayores (menor frecuencia y la sirena nos parecerá más grave).

Para las ondas electromagnéticas (que se propagan a la velocidad de la luz c = 300.000 km/s) y si la velocidad v a la que se mueve el foco emisor con respecto al observador es mucho más pequeña que la velocidad de la luz (v << c) se puede mostrar sin mucha dificultad (ver la ampliación) que z = v / c (→ v = z·c)

Es decir, el valor numérico de z es la fracción de la velocidad de la luz a la que se mueve ese objeto.

Ejercicio 18.2

Calcula la velocidad a la que se alejan o acercan los objetos que han producido los espectros A, B y C del ejercicio anterior.

Haz clic aquí para ver la solución.

Si el emisor y el receptor se alejan entre sí a una velocidad v elevada (más del 20% de la velocidad de la luz) hay que corregir la fórmula anterior por otra algo más complicada que tiene en cuenta los efectos relativistas.

Ampliación: el Efecto Doppler R es un receptor y E un emisor que se aleja de R a una velocidad v. E emite una onda electromagnética con un periodo T y una longitud de onda λ. Así que en la posición E de la figura el emisor lanza una cresta de su onda que llegará a R un tiempo después. Cuando han pasado T segundos emite la siguiente cresta pero, como se ha alejado, ahora la salida de la segunda cresta ocurre en E’, que está d metros más lejos. Como E se desplaza a una velocidad v respecto a R, resulta que d = v · T. ¿Cuánto tiempo tarda esa segunda cresta en recorrer la distancia d extra? Las ondas electromagnéticas se desplazan a la velocidad de la luz (c) por lo que tardará en ir de E a E’ un tiempo t = d / c = v · T / c = T · v/c Y esa segunda cresta será recibida en R con un retraso de T·v/c, es decir el período con el que la onda llega a R no es T, sino T’ = T + T·v/c = T · (1+v/c) El periodo se ha “estirado” en un factor 1 + v/c La longitud de onda recibida en R será λ’ = c·T’ = c·T·(1 + v/c) = λ·(1 + v/c) → λ’/λ = 1 + v/c [1] La longitud de onda también se ha “estirado” en un factor 1 + v/c Pero z = (λ’ – λ) / λ = λ’/ λ – 1 → λ’/λ = 1 + z [2] Por lo que igualando [1] y [2] resulta z = v/c

El efecto Doppler tiene muchas utilidades en Astronomía. El movimiento de rotación de una galaxia puede detectarse porque debido a él un extremo de ella se acerca a nosotros mientras que el opuesto se aleja, provocando un desplazamiento al violeta en el primer caso y al rojo en el segundo. En esta imagen de la galaxia del Triángulo (figura 18.6, en ondas de radio) se observa cómo las estrellas de la izquierda se están acercando mientras que las de la derecha se alejan.

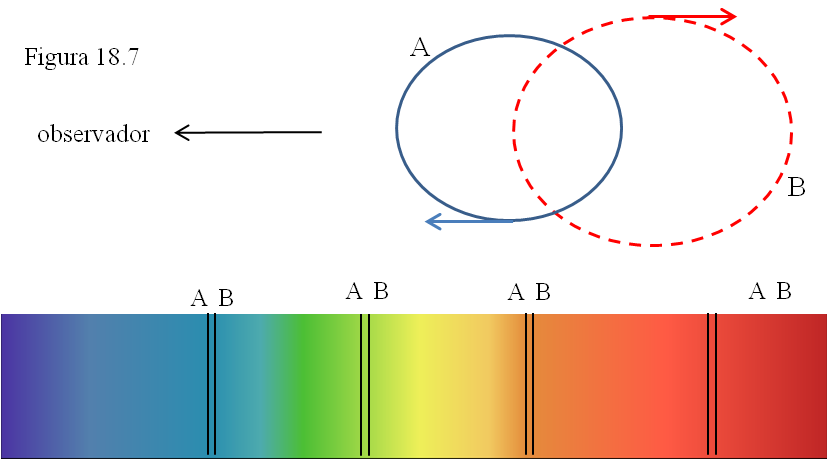
Otro comportamiento similar ocurre en las estrellas binarias espectroscópicas: son dos estrellas que orbitan la una en torno a la otra alrededor de un centro de masas común, tan cercanas entre sí que es imposible verlas separadas ni siquiera con los mejores telescopios. Sin embargo, esa rotación conjunta hace que en ciertos momentos una estrella se esté acercando a nosotros (la A en la figura 18.7) mientras la otra se aleje. Entonces en el espectro veremos que las líneas se han desdoblado en sus dos componentes, una por cada estrella.

La ley de Hubble

Entre los años 1910 y 1930 se pudieron estudiar los espectros de muchas galaxias gracias a la construcción de nuevos telescopios cada vez más grandes y potentes. La primera conclusión de esos estudios (debida al astrónomo norteamericano Vesto Melvin Slipher) fue muy sorprendente: prácticamente todas las galaxias presentan desplazamientos hacia el rojo. Suponiendo que son debidos al efecto Doppler, la conclusión es que prácticamente todas las galaxias se están alejando de nosotros, como si huyeran.

En 1929 el astrónomo estadounidense Edwin Hubble y en 1931 el propio Hubble y su colaborador Humason hicieron otro descubrimiento importantísimo. Determinaron, lo mejor que pudieron con los métodos entonces conocidos, las distancias y los desplazamientos al rojo de muchas galaxias y confeccionaron una tabla parecida a la del ejercicio 3. Luego hicieron una gráfica con los datos de la misma y encontraron una relación asombrosa.

En el eje horizontal se marcan las distancias, en megaparsec (Mpc) que es la unidad habitual en Astronomía (1 Mpc = 10⁶ pc = 3,26·10⁶ años luz = 3,26 Mal) y en el vertical tanto el desplazamiento al rojo (z) como las velocidades de alejamiento (de recesión, en km/s) deducidas. Cada galaxia se coloca en la posición que le corresponda. Los pequeños segmentos horizontales en cada punto indican la incertidumbre en la medida de sus distancias.

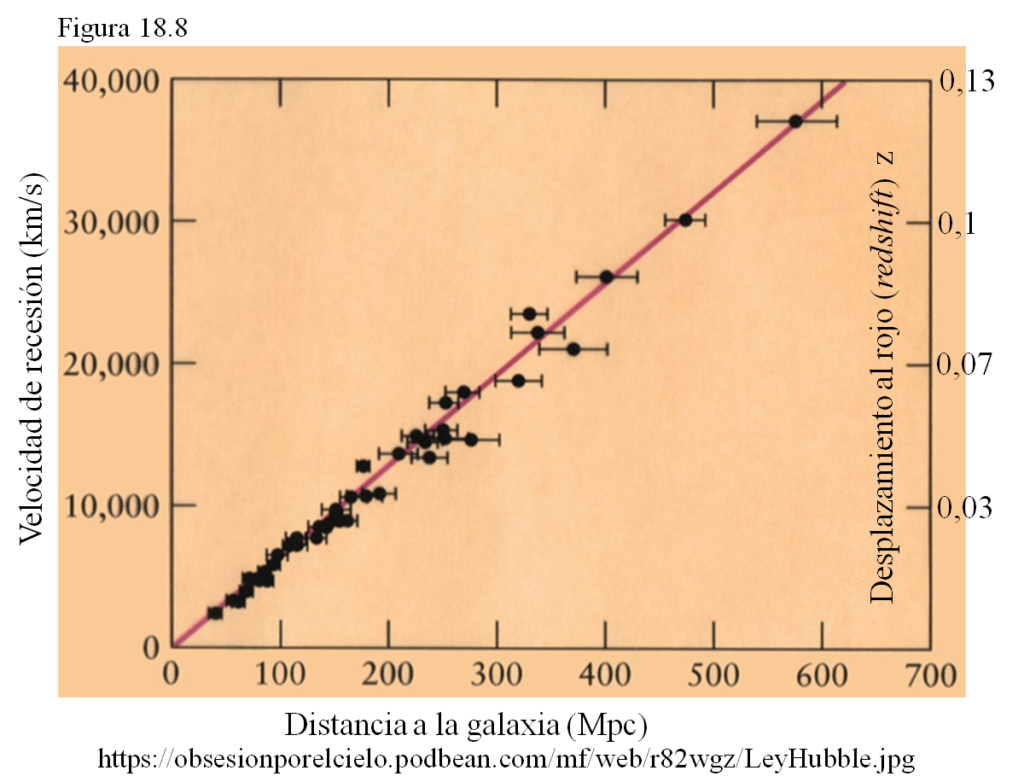
¡Resulta que todas las galaxias estudiadas se sitúan prácticamente sobre una recta! Si una galaxia está el doble de lejos que otra, la más lejana tendrá un redshift (y una velocidad) doble que la más cercana, siempre distanciándose de nosotros, del observador.

Esta es la ley de Hubble: los desplazamientos al rojo son proporcionales a las distancias. La formulación clásica, interpretando el redshift como debido al efecto Doppler, es v = H₀ · d, donde H₀ es la pendiente de esa recta, se llama la constante de Hubble y, como iremos viendo, es uno de los parámetros más importantes en Cosmología. En realidad la velocidad de recesión no se ha medido, sino calculado. Lo que se mide es el desplazamiento al rojo z. Por eso sería más correcta esta otra formulación:

z·c = H₀ · d → z = (H₀/c)·d

en la que queda más clara la proporcionalidad entre el redshift y la distancia.

Es una ley empírica, obtenida contrastando los datos del redshift z observado con las distancias calculadas a esas galaxias, con algunas dudas, mediante los métodos ya vistos de las cefeidas y de las supernovas tipo Ia. Sabemos que es válida, porque se ha podido verificar, para galaxias no muy lejanas (hasta unos 600 Mpc equivalentes a 2.000 Mal) y valores de z < 0,15, pero más allá se ha comprobado que desaparece la proporcionalidad.

Ejercicio 18.3

Dada la importancia máxima de la ley de Hubble te proponemos esta tarea que es, en esencia, repetir lo mismo que hizo el brillante astrónomo norteamericano. Con el añadido de que podrás hacer una estimación de ese parámetro crucial (la constante de Hubble H₀).

En esta tabla se dan las distancias y los desplazamientos al rojo (z) para los principales cúmulos de galaxias próximos a nosotros.

Cúmulo	Distancia	z	z·c = v	v/d
	(Mpc)		(km/s)
Virgo	15	0,003
Centaurus	45	0,011
Cancer	65	0,015
Coma	95	0,022
Leo A	145	0,033
Hercules	165	0,038
Pegasus II	180	0,042
Cygnus A	220	0,050

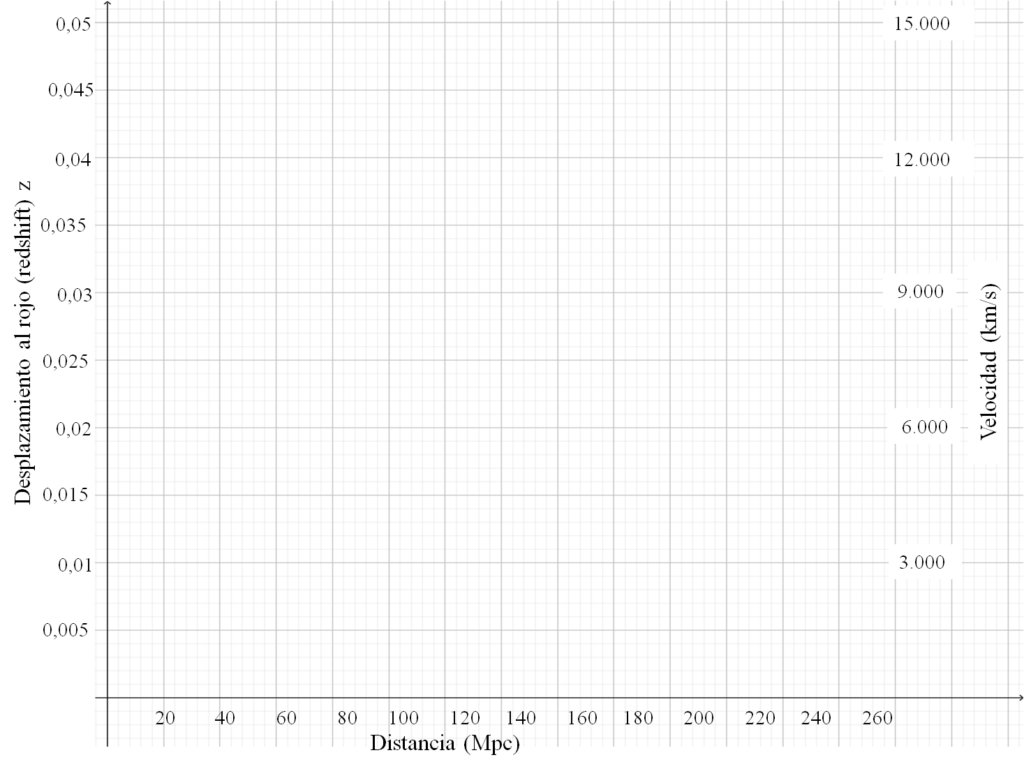
1. Utilizando los datos de la tabla, señala en este gráfico (haz clic aquí para imprimirlo) el punto que corresponde a cada uno de los cúmulos de galaxias.
2. Traza en tu gráfica una recta que pase por el origen de coordenadas y por todos los puntos que puedas.
3. Utilizando la gráfica, averigua el desplazamiento al rojo z de una galaxia que esté situada a 120 Mpc.
4. Ahora vamos a hacerlo al revés: si observamos en el espectro de una galaxia un desplazamiento de las rayas oscuras z = 0,03, ¿a qué distancia está esa galaxia?
5. Completa la tercera y la cuarta columna, con los cocientes v/d = H₀ de cada cúmulo de galaxias. Deberías obtener resultados bastante parecidos (la constante de Hubble H₀). Las pequeñas oscilaciones de los valores en esa columna se deben a los errores e incertidumbres en la medición de las distancias.

Haz clic aquí para ver la solución.

El valor preciso de la constante de Hubble H₀ es decisivo en Cosmología. Nos va a servir, entre otras cosas, nada menos que para determinar la edad del Universo. La medición del desplazamiento al rojo de las líneas espectrales se hace con una altísima precisión. En cambio, no ocurre lo mismo con el cálculo de las distancias a las galaxias o cúmulos de galaxias en el que sigue habiendo algunas dudas.

Hubo un largo debate sobre ello. Algunos equipos daban H₀ = 50, otros más bien se inclinaban por valores de H₀ = 100. Se trabajó y se sigue investigando intensamente para tratar de ajustarlo más. Actualmente, los últimos resultados parecen estar de acuerdo en que el valor de H₀ debe estar comprendido entre 67 y 74. Podemos aceptar H₀ = 70 km/s/Mpc como un valor de compromiso por el momento, a la espera de nuevas mediciones.

Con la ley de Hubble en la mano ya totalmente formulada

v = z·c = 70·d

disponemos ahora de otra herramienta para calcular distancias a galaxias no muy lejanas sin tener que esperar a detectar cefeidas o a que explote alguna supernova en ellas. Ya hemos dicho que la medida del desplazamiento al rojo, del redshift z es muy fiable a partir del espectro de una galaxia. Ahora, a partir de ese dato ya será posible hallar la distancia de esa galaxia.

Ejemplo En una galaxia del supercúmulo de Horologium (una constelación austral) la línea espectral que en el laboratorio tiene una λ0 = 500 nm se observa desplazada al rojo con una λ = 533,5 nm. Calculemos primero el valor de z: z = 33,5 / 500 = 0,067 Luego la velocidad de recesión de esa galaxia será z·c = 300.000 · 0,067 = 20.100 km/s Y, finalmente, sustituyendo en la fórmula de la ley de Hubble: 20.100 = 70 · d → d = 20.100 / 70 = 287 Mpc = 936 Mal

Ejercicio 18.4

Del espectro de las galaxias del lejano cúmulo llamado Hydra II deducimos que su desplazamiento al rojo es z = 0,2. Este valor de z está algo más allá del rango de validez de la ley de Hubble. Nos arriesgaremos un poco.

1. ¿Cuál es su velocidad de recesión?
2. ¿A qué distancia están esas galaxias?

Haz clic aquí para ver la solución.

Estructura a gran escala del Universo

De esta forma se han podido realizar sondeos profundos del Universo para intentar descubrir cómo se organizan en el espacio los cúmulos y supercúmulos de galaxias.

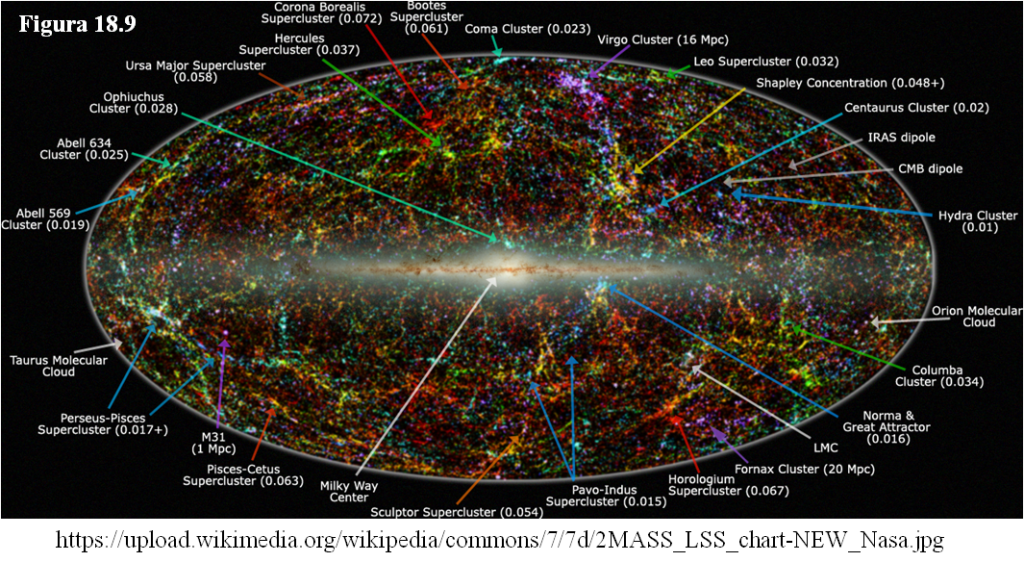
En esta imagen (figura 18.9) de nuestro entorno se sitúan todos los cúmulos con z < 0,075 (o sea, bastante cercanos), en azul o violeta los más próximos (como el de Virgo) y en rojo los más lejanos (como el de Horologium). Entre paréntesis se indica para cada uno su redshift z o, si están muy próximos, directamente su distancia. El formato es el que ya vimos en el tema 16, con el plano central de la Vía Láctea haciendo de ecuador. La elipse es la proyección de toda la esfera celeste.

No se aprecia mucha estructura, todo lo más que hay zonas de más concentración y otras de menos. Sí parece que hay cierta tendencia de los cúmulos a formar como alineaciones, como filamentos.

Haz click sobre la imagen para ampliarla.

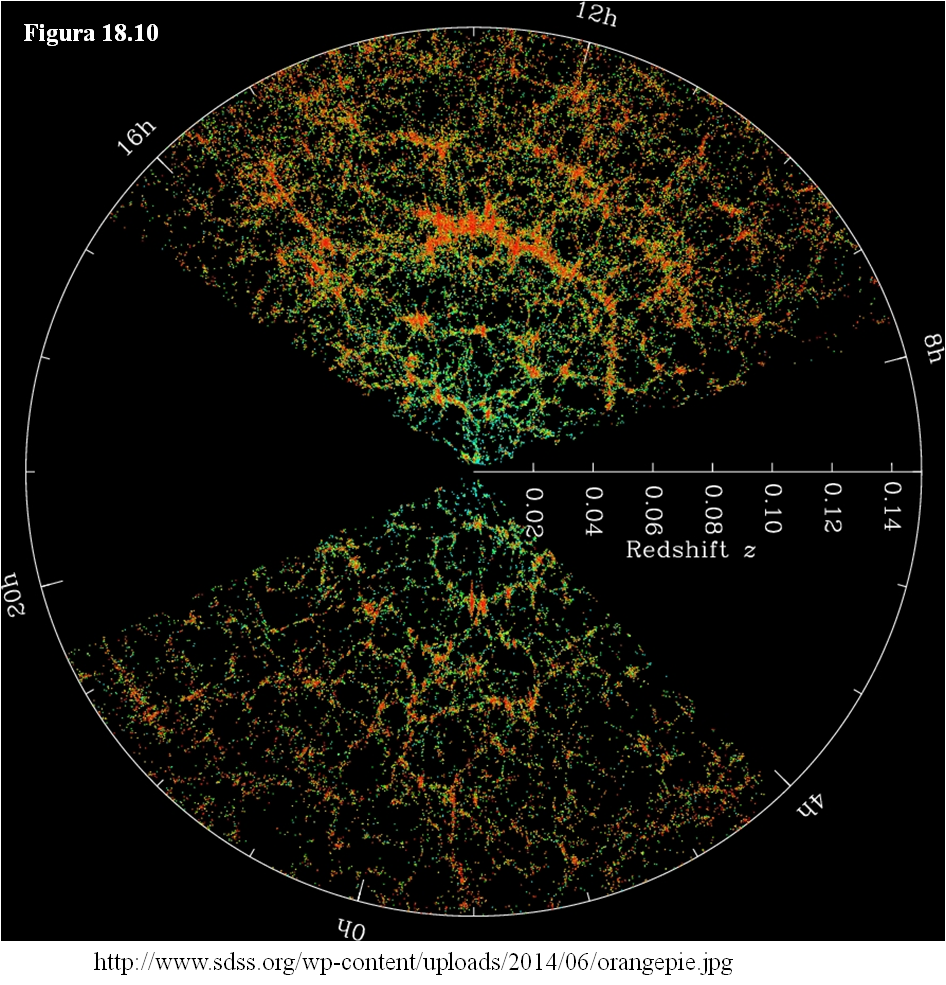
En este otro mapa (del Sloan Digital Sky Survey), que llega ya al límite de posibilidades de la ley de Hubble (z < 0,15), sí que se ve en la parte superior (hacia las 12 h de ascensión recta) una imponente concentración alargada en horizontal (las zonas naranjas son de alta densidad de galaxias, las zonas verdes también contienen galaxias, aunque no tantas, y las oscuras son espacios desprovistos de ellas). Y sí que se muestra con claridad que los cúmulos forman alineaciones con grandes huecos vacíos en medio. En tres dimensiones la apariencia podría ser la de burbujas vacías en cuya superficie se aglutinan las galaxias.

Ejercicio 18.5

¿Cuál es el radio del mapa del Sloan Digital Sky Survey, en millones de años luz?

Haz clic aquí para ver la solución.