- Portada
- Presentación
- Tema 1. Geografía celeste
- Tema 2. Movimiento de rotación
- Tema 3. Coordenadas ecuatoriales
- Tema 4. El modelo de las dos esferas
- Tema 5. La Luna
- Tema 6. Las 4 estaciones
- Tema 7. Relojes de Sol
- Tema 8. Calendarios y eclipses
- Tema 9. Los Planetas. Cinemática
- Tema 10. El Sistema Solar.
- Tema 11. La Tierra y la vida
- Tema 12. Prismáticos y telescopios
- Tema 13. Una noche de observación
- Tema 14. Distancia a las estrellas
- Tema 15. Vida y muerte de las estrellas
- Tema 16. La Vía Láctea
- Tema 17. Galaxias
- Tema 18. Cosmología
- Anexo. Grandes astrónomos
- Bibliografía y Webs
18.3 La expansión del Universo
La característica más desconcertante de la ley de Hubble – la velocidad de recesión de una galaxia es proporcional a la distancia que la separa de nosotros – se puede expresar con una pregunta muy sencilla: ¿por qué precisamente de nosotros? ¿Qué magia tenemos para que las galaxias nos rehúyan? ¿Y cómo saben las galaxias a qué distancia se hallan de nosotros para guiar sus pasos de un modo acorde?
Isaac Asimov, El Universo
¿Qué impresión sacamos de la ley de Hubble? Parece que las galaxias o los cúmulos de galaxias se separan de nosotros y que sus distancias aumentan más cuanto más lejos estén. Es como si fuéramos el centro de esa fuga.
Pero ya sabemos que estas apariencias son engañosas: la Tierra no es el centro del Universo, ni el Sol está en el centro de la Vía Láctea, ni la Vía Láctea destaca especialmente entre las demás galaxias. Debe haber alguna explicación lógica para esa aparente posición central. No tiene sentido que seamos unos observadores privilegiados.
Buscamos un modelo, una teoría de todo el Cosmos, en la que encajen todas las pistas de que disponemos. No solamente la ley de Hubble. También tenemos que dar cuenta coherentemente de lo recogido en el primer apartado de este tema, las llamadas observaciones “ingenuas”. ¿Cómo puede ser que el Universo se esté enfriando pese a la energía difundida por las estrellas? ¿Y la paradoja de Olbers?
Otra cuestión preocupaba a los teóricos. Si el Universo está repleto de materia y la gravedad ejerce su atracción, ¿por qué no se han ido aglomerando todas las galaxias? ¿Cómo es que no se ha producido un colapso gravitatorio de todas ellas?
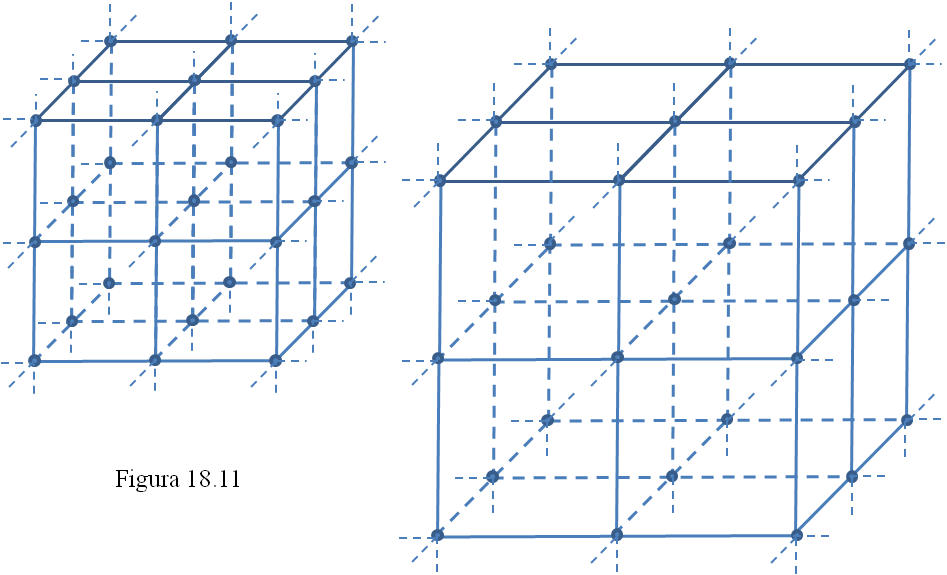
La respuesta a tantos interrogantes fue abriéndose paso y hacia mediados del siglo XX emergió la idea de la expansión del Universo. Es todo el Cosmos el que está dilatándose y creciendo a medida que transcurre el tiempo. Si imaginamos una red de coordenadas tridimensional (figura 18.11), cada galaxia, o cada cúmulo de galaxias, ocupa una posición, unas coordenadas, en esa red. Pero toda la retícula está creciendo de forma que la unidad (la arista de cada cubo, el lado de cada cuadrado) se está haciendo mayor. Las galaxias no se dilatan (los puntos de la figura 18.11 no han crecido) pero sí sus distancias.
Así puede comprenderse por qué el Universo se sigue enfriando. El calor emitido por las estrellas tiene que calentar un espacio cada vez más grande y no alcanza para ello. Es como tener un horno con una vela dentro. En principio la vela debería hacer aumentar la temperatura del horno, pero ¿qué sucede si éste es cada vez más y más grande? Si el ritmo de expansión es suficientemente alto la llama de la vela será incapaz de contrarrestar el enfriamiento debido a la expansión.
Lo mismo sucede con el presunto colapso gravitatorio; también aquí si el ritmo de expansión es lo bastante intenso puede vencer a la atracción gravitatoria. Ésta sí que es capaz de mantener unidas las grandes estructuras, las galaxias y los cúmulos de galaxias cuyas dimensiones no se alteran por causa de la expansión .
Más adelante (en el apartado “Desplazamiento al rojo cosmológico”) veremos con detalle cómo la expansión puede dar cuenta del redshift de la luz que nos llega de las galaxias y de la ley de Hubble, así como de la paradoja de Olbers.
Modelos de la expansión
- Imagina una cinta elástica en la que hay unas marcas igualmente espaciadas (10 cm) y en algunas de ellas hemos pegado un círculo rojo. Ahora vamos estirando poco a poco la cinta y en diez segundos se hace bastante más larga, arrastrando con ella los círculos rojos que permanecen en sus marcas (que están al final a 17 cm una de otra).

Los puntos rojos no se han movido, ha sido toda la cinta la que se ha hecho más larga ¿Qué es lo que nos parece ver desde A?
Hagamos una pequeña tabla. d0 es la distancia inicial para t = 0 entre A y los otros puntos y d1 es la distancia final (t = 10 s), con la cinta estirada, Δd es el incremento en la distancia y Δd/t es el ritmo de aumento de las distancias. Todas las distancias en cm y Δd/t en cm/s.
| d0 | d1 | Δd | Δd/t | |
| B | 10 | 17 | 7 | 0,7 |
| C | 40 | 68 | 28 | 2,8 |
| D | 60 | 102 | 42 | 4,2 |
Desde A se ve que la distancia al punto más cercano (B) aumenta a 0,7 cm/s, la distancia a C (que está más lejos) también crece a mayor ritmo (a 2,8 cm/s) y la distancia al más alejado (D) es la que aumenta más acusadamente (a 4,2 cm/s). Más o menos lo mismo que vemos nosotros hacer a las galaxias y cúmulos. ¿Es A el centro?
Veamos qué pasa si repetimos la tabla, ahora anotándolo todo desde C:
| d0 | d1 | Δd | Δd/t | |
| A | 40 | 68 | 28 | 2,8 |
| B | 30 | 51 | 21 | 2,1 |
| D | 20 | 34 | 14 | 1,4 |
¡Exactamente la misma tónica! La cinta hace el papel del Universo (pero de una sola dimensión) y los círculos rojos serían las galaxias que no se han movido de sus marcas. Desde cada punto de observación parece que todas se alejan precisamente de ese punto.
Ejercicio 18.6
Haz una tabla como las anteriores, desde B y desde D.
Haz clic aquí para ver la solución.
- Hagamos otra simulación, pero ahora en un universo de dos dimensiones.

En este primer dibujo (A) se han colocado unos cuantos puntos. Cada uno sería una galaxia (o cúmulo) y se han situado de forma que simulen la distribución que parecen tener (figura 18.10), agrupadas en líneas, en filamentos, que dejan en medio huecos vacíos. Hay cuatro señalados en rojo, ahora se verá por qué.
La figura 18.14 es la misma que la anterior pero un poco ampliada. Ningún punto se ha movido, es todo el dibujo en bloque el que se ha hecho más grande (más ancho y más alto).

La verdad es que no se aprecia diferencia alguna. No se nota pero sí, está un poco más ampliado (un 5%).
La sorpresa viene cuando superponemos ambas figuras A y B haciendo coincidir el cúmulo rojo situado arriba a la izquierda:
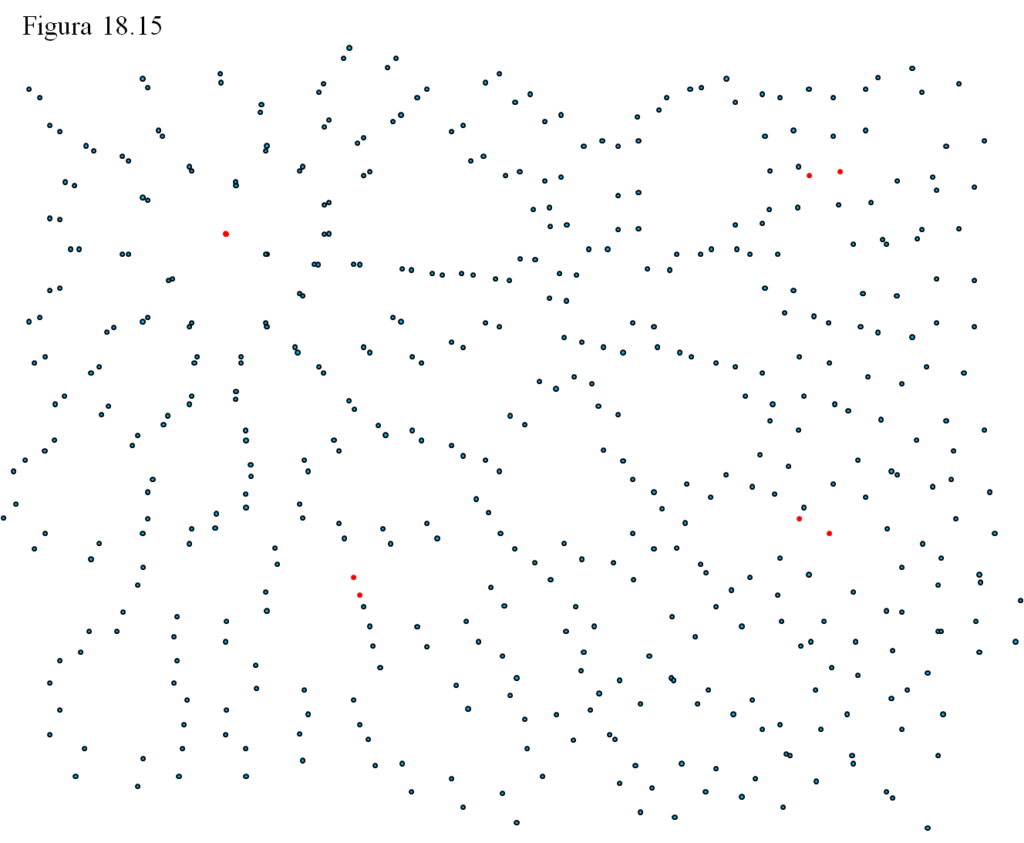
La sensación de fuga desde el punto rojo es irresistible. Desde allí todas las galaxias parecen haberse desplazado. Muy poco las más cercanas, pero más y más a medida que nos vamos alejando.
Pero los puntos no se han desplazado, cada uno sigue estando en la misma posición, en las mismas coordenadas que al principio. Ha sido todo el dibujo, todo el sistema de referencia, toda la red de coordenadas la que se ha dilatado.
Y lo mismo va a pasar si hacemos coincidir las dos figuras en cualquier otro cúmulo (con esa coincidencia estamos suponiendo que nosotros vemos ese cúmulo quieto, es decir, que estamos en él). Veamos ahora desde el punto rojo de la esquina inferior derecha:
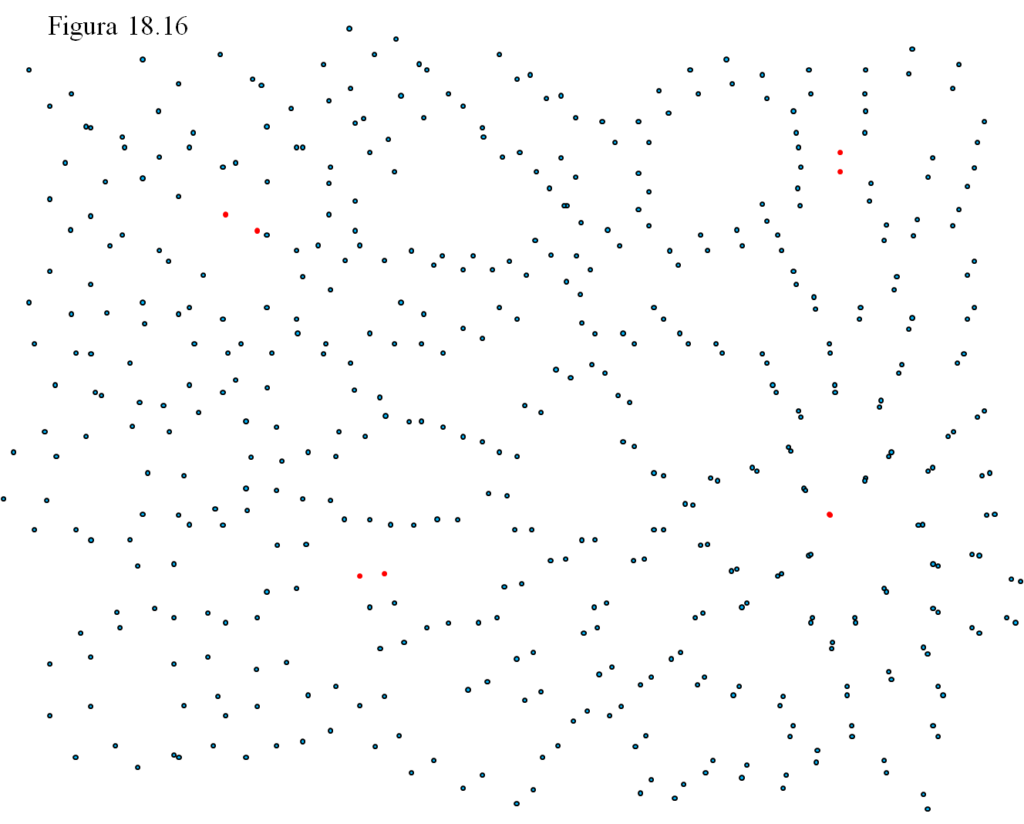
¡Lo mismo! Todo parece alejarse de nosotros, estemos donde estemos, poco las galaxias cercanas y más a medida que nos alejamos.
No es que todo huya de nosotros, es que todo se aleja de todo. Es el propio espacio el que está dilatándose arrastrando con él a las galaxias de tal modo que desde cualquiera de ellas el espectáculo de la recesión es absolutamente similar.
En esta animación se muestra cómo cada galaxia está situada en un punto de la red de coordenadas espaciales. Es la propia red la que está constantemente dilatándose y llevando consigo a cada una de ellas.
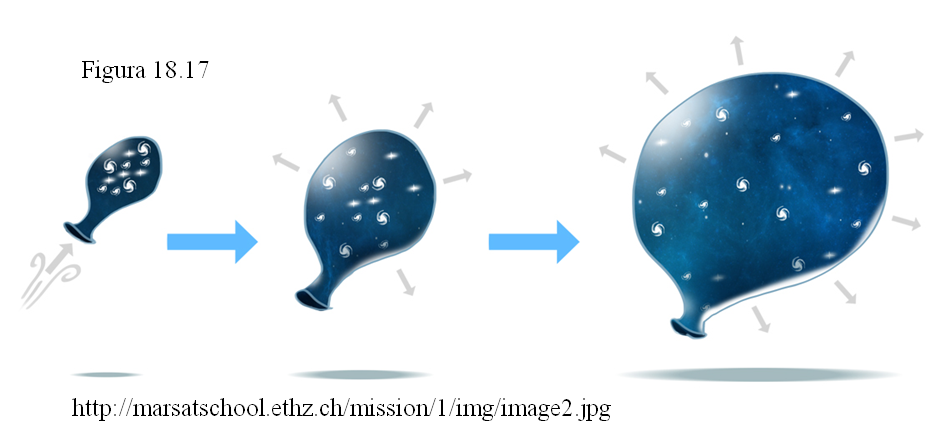
- Otras dos analogías suelen utilizarse para mostrar esta notable propiedad de nuestro Universo. Una es un globo en el que se han pegado unos pequeños círculos de papel que van a representar las galaxias. A medida que el globo se hincha todos los círculos se van separando unos de otros, aunque los círculos no se hacen más grandes, del mismo modo que las galaxias se separan unas de otras pero ellas mismas se mantienen con su tamaño invariable.
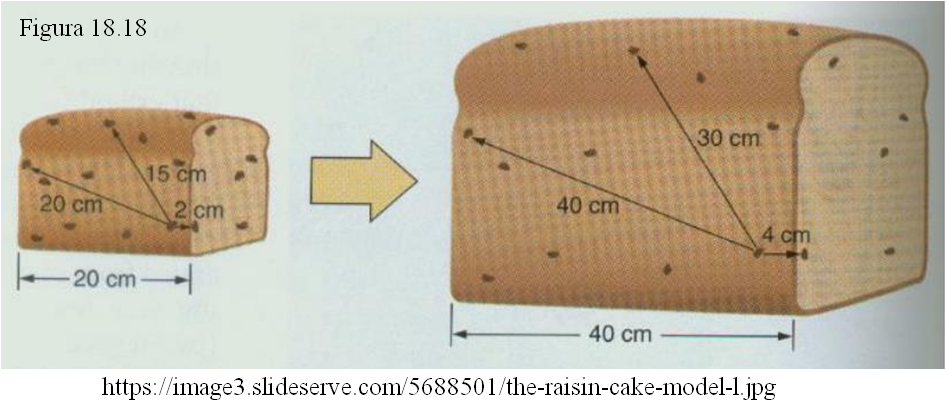
- El otro modelo es el de un pastel en cuya masa se han colocado, desperdigadas por su interior, unas cuantas pasas. Al irse calentando en el horno el pastel “sube”, toda la masa se dilata, se expande en todas direcciones y las pasas/galaxias se van separando entre sí.
Desplazamiento al rojo cosmológico
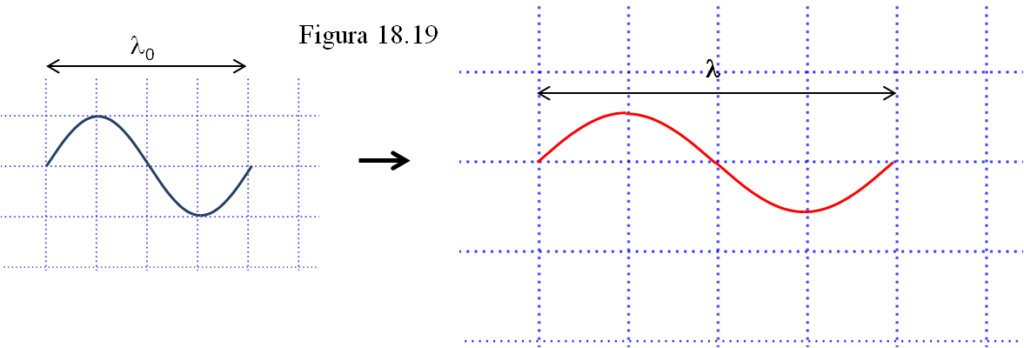
La interpretación correcta del corrimiento al rojo de las líneas espectrales es que, al viajar por un espacio que crece constantemente, cualquier fotón, cualquier onda, también se dilata en su recorrido y exactamente al mismo ritmo que lo hace el Universo. Un fotón que salió de una galaxia con una λ0 = 520 nm (verde) se irá “estirando” a medida que el espacio lo hace, con lo que su longitud de onda aumenta y puede llegarnos con una λ = 650 nm (rojo).
Al igual que las galaxias se van distanciando, un fotón que viaja por la retícula universal va teniendo una longitud de onda cada vez mayor a medida que el espacio entre las líneas de la retícula va creciendo.
En esta animación se simula el recorrido de un fotón desde que sale (violeta) de la galaxia G hasta que alcanza, ya convertido en rojo, a un observador O.
La clásica visión de este estiramiento como debido al efecto Doppler a causa de la velocidad de alejamiento de la galaxia emisora debe dejarse de lado.
Además, esta interpretación nos va a permitir calcular en qué factor ha crecido el Universo desde que el fotón se emitió hasta que fue registrado por nuestros equipos. Supongamos, como antes, que esa lejana galaxia emite un fotón verde (λ0 = 520 nm) y que nos llega a nosotros con λ = 650 nm (ya en la zona roja del espectro) pero siempre ocupa (figura 18.19) cuatro cuadrículas de la red. Pues eso quiere decir que si la distancia entre dos puntos de la malla cósmica antes media 520 ahora mide 650 (sean nanómetros o millones de años luz), todas las distancias entre vértices de la retícula han aumentado en la misma proporción): un crecimiento de 650 / 520 = 1,25 o, de otra manera, el Universo se ha estirado un 25%.
El cociente λ / λ0 nos da el factor por el que se ha multiplicado el tamaño de la unidad de la malla de coordenadas desde que el fotón fue despedido de aquella lejana galaxia hasta que nosotros lo hemos recogido. Y es bastante fácil llegar a una formulación general de la expansión en términos del desplazamiento al rojo z.
z = (λ – λ0) / λ0 = (λ / λ0) – 1 → λ / λ0 = z + 1
Los modelos cosmológicos establecen hipótesis sobre el ritmo de la expansión mediante el término factor de escala espacial R(t) que es función del tiempo. Si en el instante t1 la galaxia G emite un fotón con una λ1 y un tiempo después (t2) es detectado en otra galaxia G’ con una λ2, entonces en el intervalo (t1,t2) el universo se ha expandido en un factor λ2/λ1 y lo mismo habrán hecho las distancias entre G y G’. El factor de escala espacial también se habrá multiplicado por ese mismo factor:
R(t2) / R(t1) = λ2 / λ1 = d2 / d1
Siendo d1 la distancia entre G y G’ en el instante t1 y d2 = d(G,G’) en t2.
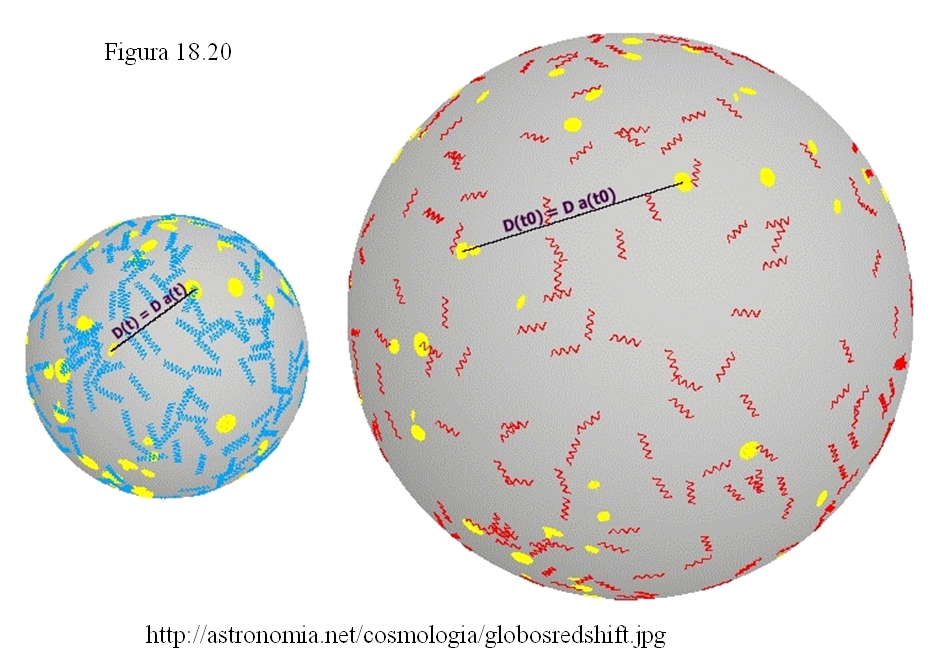
En la figura 18.20 aparece una superficie esférica que representa el Universo (solo la superficie, como en el modelo del globo que se hincha) en un instante t (a la izquierda) y en el instante actual (t0) a la derecha. Los fotones azules de la izquierda (con longitud de onda λ) se han estirado y convertido en rojos a la derecha (λ0). Las distancias entre las galaxias (círculos amarillos) también han aumentado en la misma proporción que la longitud de onda.
En estos dibujos el redshift es z = 1, por lo que λ0 / λ = 1 + z = 2, es decir, las distancias entre dos galaxias típicas cualesquiera del Universo actual (t0) son el doble que las correspondientes a un tiempo anterior t. El factor de escala espacial habrá variado de igual forma:
R(t0) / R(t) = λ0 / λ = D(t0) / D(t)