- Portada
- Presentación
- Tema 1. Geografía celeste
- Tema 2. Movimiento de rotación
- Tema 3. Coordenadas ecuatoriales
- Tema 4. El modelo de las dos esferas
- Tema 5. La Luna
- Tema 6. Las 4 estaciones
- Tema 7. Relojes de Sol
- Tema 8. Calendarios y eclipses
- Tema 9. Los Planetas. Cinemática
- Tema 10. El Sistema Solar.
- Tema 11. La Tierra y la vida
- Tema 12. Prismáticos y telescopios
- Tema 13. Una noche de observación
- Tema 14. Distancia a las estrellas
- Tema 15. Vida y muerte de las estrellas
- Tema 16. La Vía Láctea
- Tema 17. Galaxias
- Tema 18. Cosmología
- Anexo. Grandes astrónomos
- Bibliografía y Webs
2.4 Semicírculos de visibilidad
El primer paso para comprender los movimientos celestes ya lo hemos dado: utilizar algunos de esos burdos instrumentos para observar y anotar tablas como la anterior; está claro que también lo podemos hacer con la Luna, los planetas o las estrellas. Ahora hay que escudriñar esas tablas, analizarlas, reconociendo aquellas características que sean destacables, buscando en ellas pautas, regularidades.
En la tabla anterior, así de entrada destaca la perfecta simetría de las alturas del Sol, de hora en hora, con respecto al mediodía (13 horas, máxima altura de 33°). El acimut en ese momento es de 180°: el Sol está justo hacia el Sur. Pero poco más podemos deducir de este primer análisis. Generalmente un gráfico suele ayudar a la hora de descubrir esas pautas, esas leyes que intentamos localizar. Para visualizar esas tablas (con las coordenadas horizontales de un astro a lo largo de varias horas) vamos a utilizar unas plantillas llamadas “semicírculos de visibilidad”.
Podemos y debemos imaginar que todo el cielo parece una semiesfera cristalina, transparente, que nos rodea por todas partes por encima del horizonte. Esta cúpula, esta campana, está fija y sobre ella, como si fuera una pantalla de cine, todos los astros van circulando describiendo unas trayectorias que son las que queremos investigar.
En la semiesfera celeste visible el círculo NESW es el horizonte de un observador O, cuyo cenit es el punto z. Podemos trazar una serie de “paralelos” y “meridianos”; los “paralelos” lo son al horizonte y se llaman almicantarats (en rojo en la figura 2.10) y los “meridianos” son perpendiculares al horizonte, pasan por el cenit z y se llaman verticales (en azul). Al semicírculo WzE se le llama primer vertical. Esta red de líneas corresponde a las coordenadas horizontales: todos los puntos de un almicantarat tienen la misma altura, mientras que todos los puntos de un vertical tienen igual acimut.
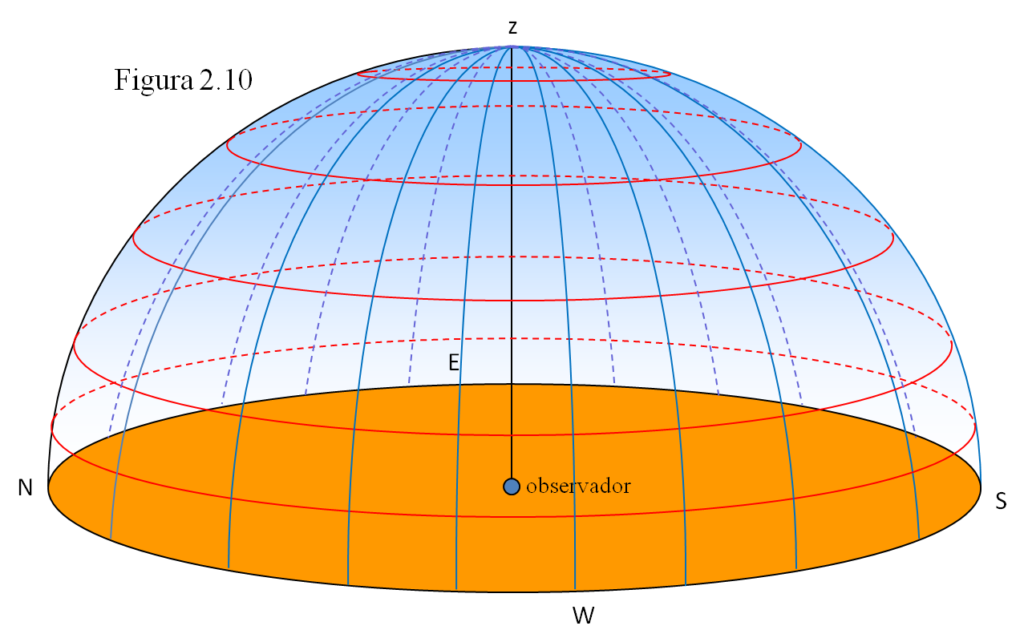
Si nos ponemos mirando hacia el Norte veremos a nuestra derecha el punto cardinal Este, a la izquierda el W y arriba del todo, encima de nosotros, el cenit z. Podemos representar lo que vemos mediante esta plantilla, el semicírculo de visibilidad Norte. Las líneas que parten del cenit z y llegan hasta el horizonte son los verticales y nos indican el acimut (cuya graduación aparece bajo la línea del horizonte); las otras líneas son los almicantarats que empiezan casi paralelos al horizonte y se van curvando a medida que suben y se acercan al cenit; se muestra la graduación de dos de ellos, los de 30º y 60º de altura.
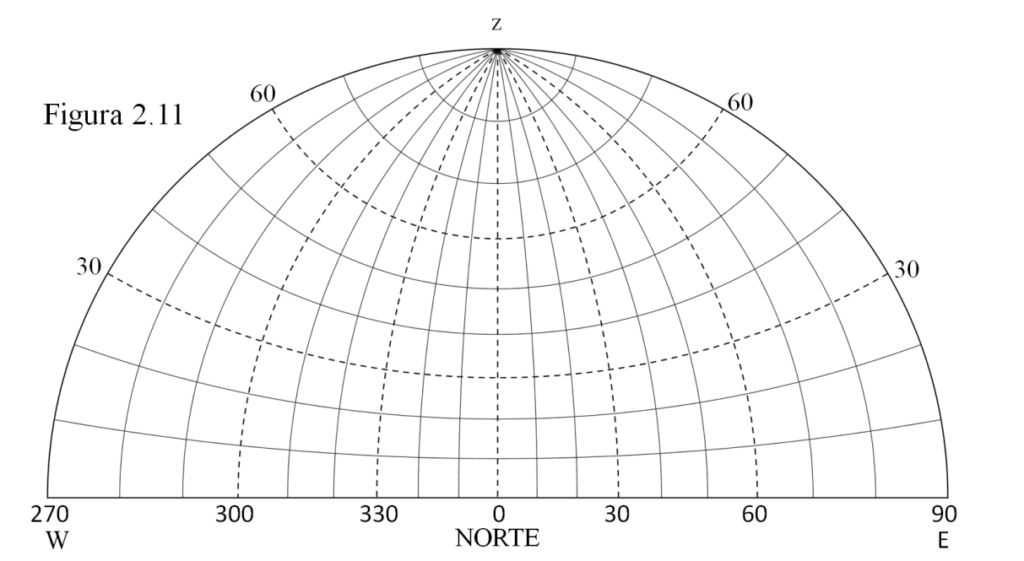
Supongamos que, con nuestro teodolito, hemos medido las coordenadas horizontales de Capella a las 10 de la noche y que han resultado ser: acimut 323º; altura 10º. Entonces podemos situar a Capella en su posición gracias a la red de líneas del semicírculo:

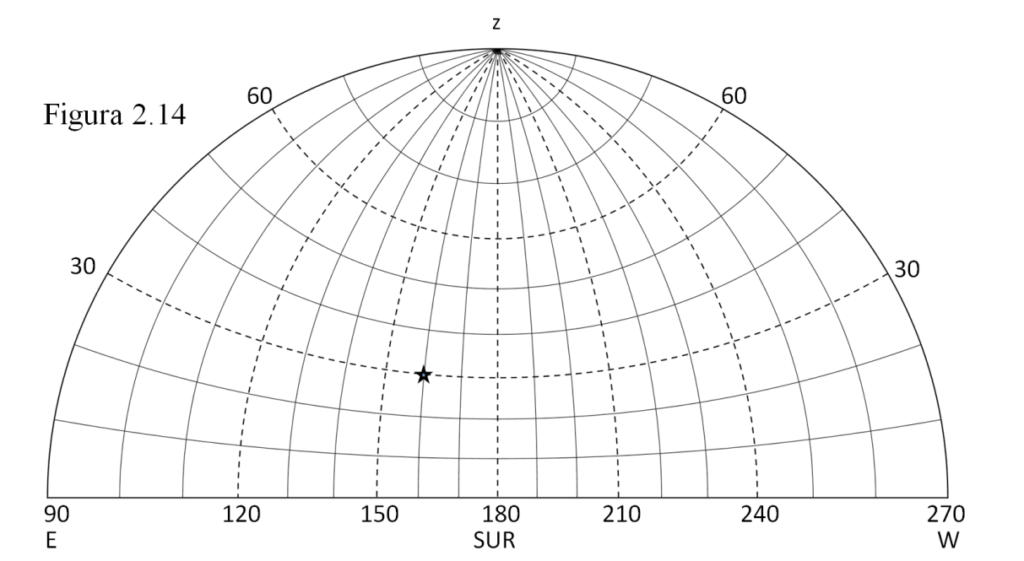
De forma simétrica se construye el semicírculo de visibilidad Sur: si nos situamos mirando al mediodía, entonces el Este quedará a la izquierda y el W a nuestra derecha.
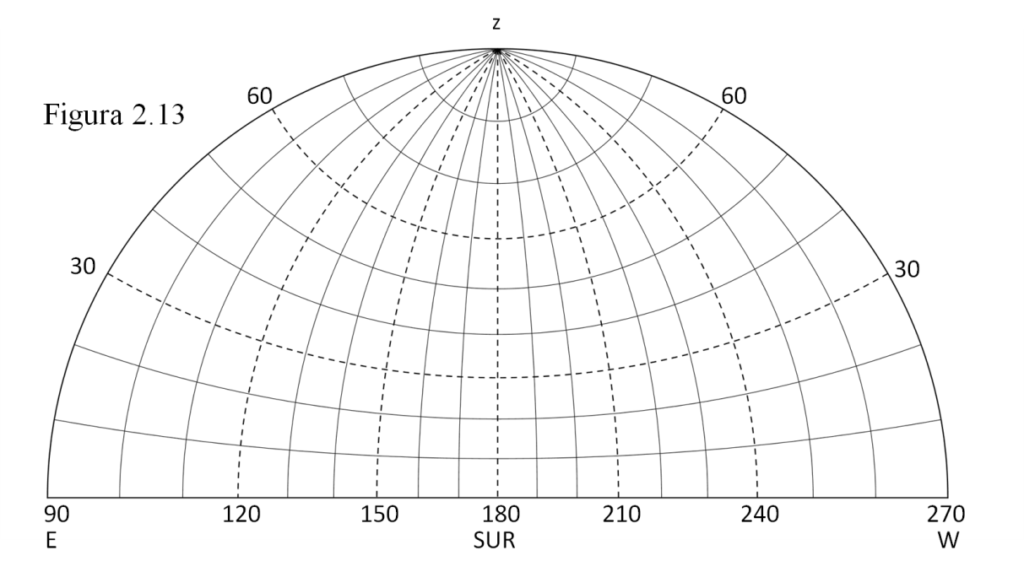
Otro ejemplo: medimos las coordenadas de Sirio en un momento dado y son 160º de acimut y 30º de altura. No hay más que situarla en su posición:
Así, ahora disponemos de unas plantillas a las que podemos trasladar las posiciones del Sol, Luna, estrellas o planetas con facilidad si conocemos sus coordenadas horizontales acimut y altura a lo largo de varias horas para ver cuál es su trayectoria aparente por encima del horizonte.
Ejercicio 2.2
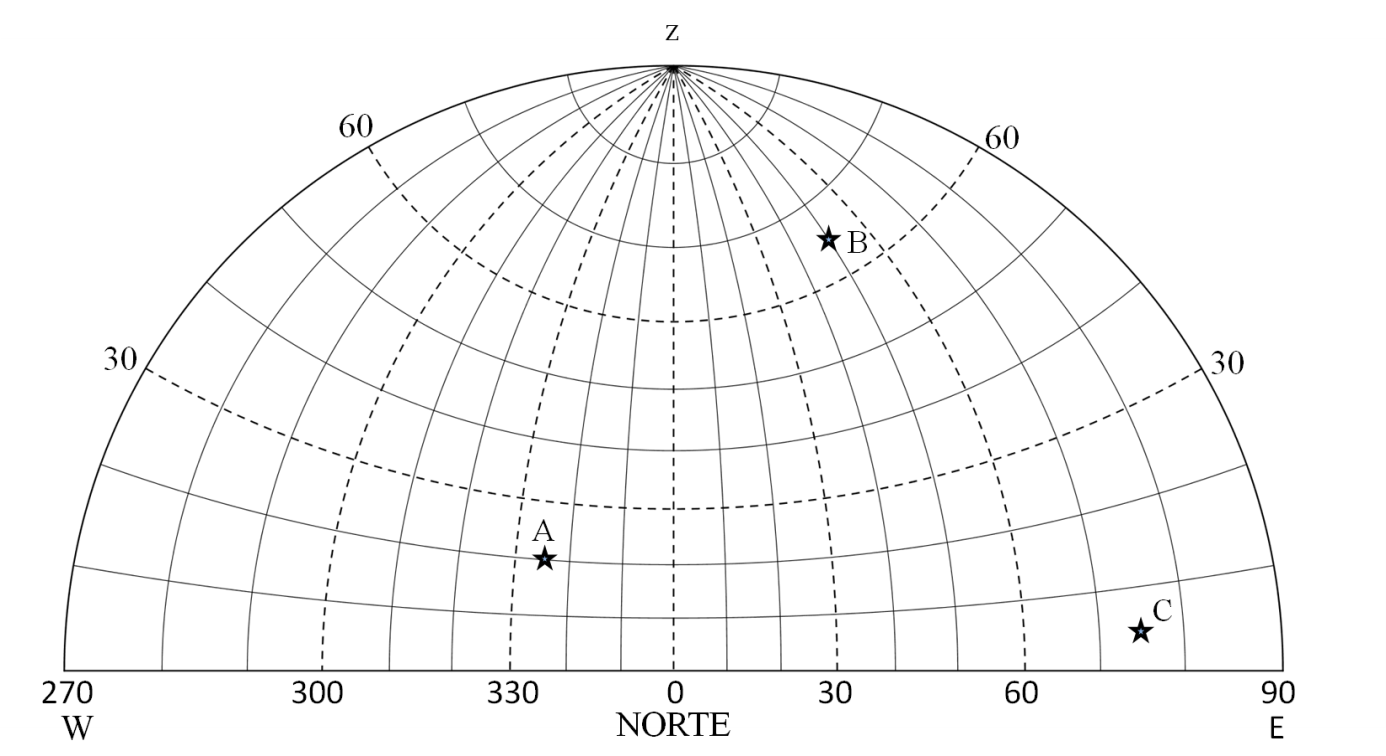
Determina las coordenadas horizontales de los puntos que aparecen en estos dibujos:

Haz clic aquí para ver la solución.
Ejercicio 2.3
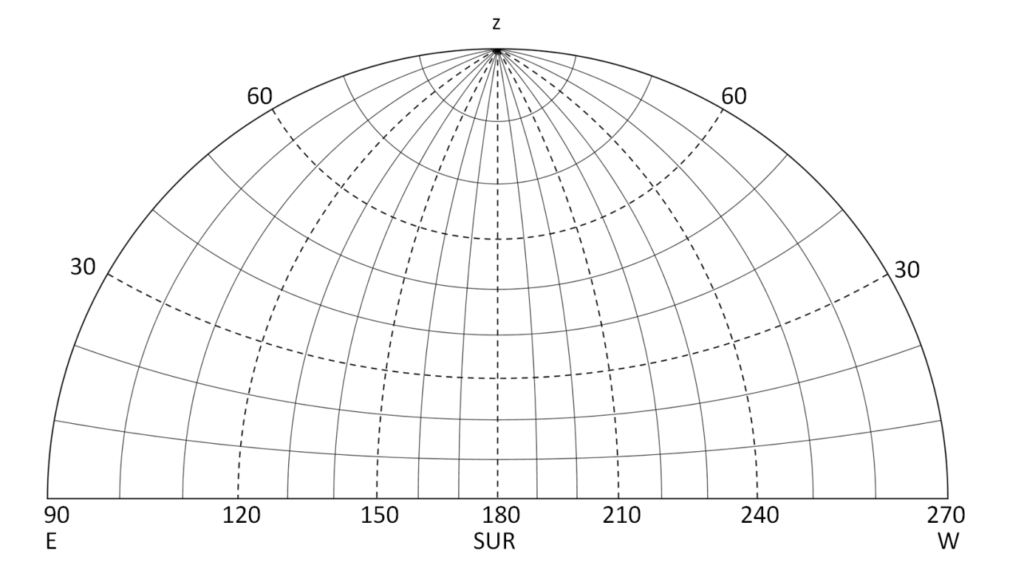
En esta tabla se muestran las coordenadas horizontales de Venus el 22 de enero de 1985, durante las pocas horas que fue visible después de la puesta del Sol:
| Hora | 19 | 20 | 21 | 22 |
| Acimut | 227 | 241 | 252 | 262 |
| altura | 34 | 25 | 14 | 3 |
Y en esta otra aparecen las posiciones de Júpiter la noche del 8/9 de marzo de 2016:
| hora | 20 | 21 | 22 | 23 | 0 | 1 | 2 | 3 | 4 | 5 |
| Acimut | 91 | 101 | 112 | 127 | 145 | 169 | 195 | 218 | 236 | 249 |
| Altura | 10 | 22 | 33 | 43 | 51 | 55 | 55 | 50 | 41 | 31 |
Traslada todos estos datos al siguiente semicírculo (pulsa aquí para imprimirlo):
Haz clic aquí para ver la solución.
Ejercicio 2.4
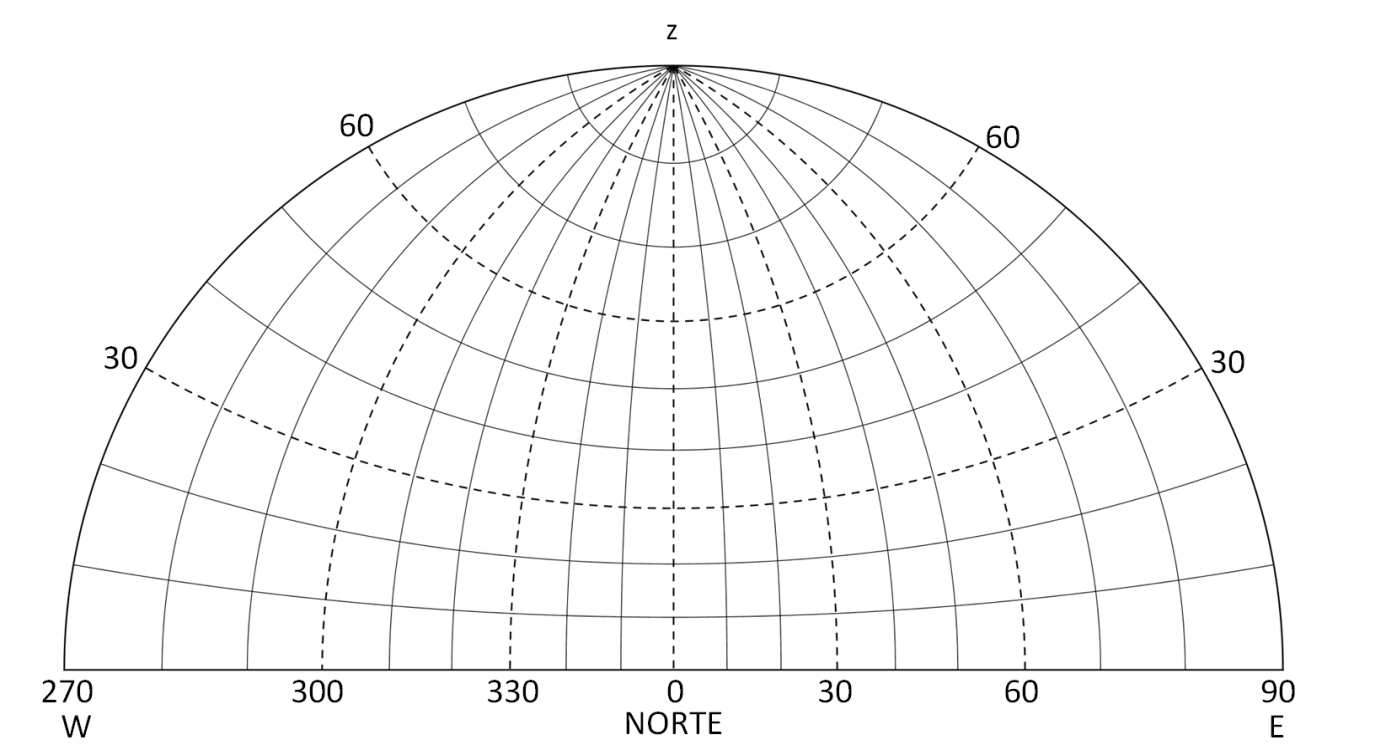
Esa misma noche del 8/9 de marzo apuntamos el acimut y la altura de Shedar (α Cas):
| hora | 20 | 21 | 22 | 23 | 0 | 1 | 2 | 3 | 4 | 5 |
| Acimut | 316 | 320 | 325 | 331 | 338 | 345 | 353 | 2 | 10 | 18 |
| Altura | 39 | 31 | 24 | 18 | 13 | 10 | 8 | 7 | 8 | 11 |
Ahora necesitamos el semicírculo Norte (pulsa aquí para imprimirlo). Dibuja en él la trayectoria de Shedar.
Haz clic aquí para ver la solución.
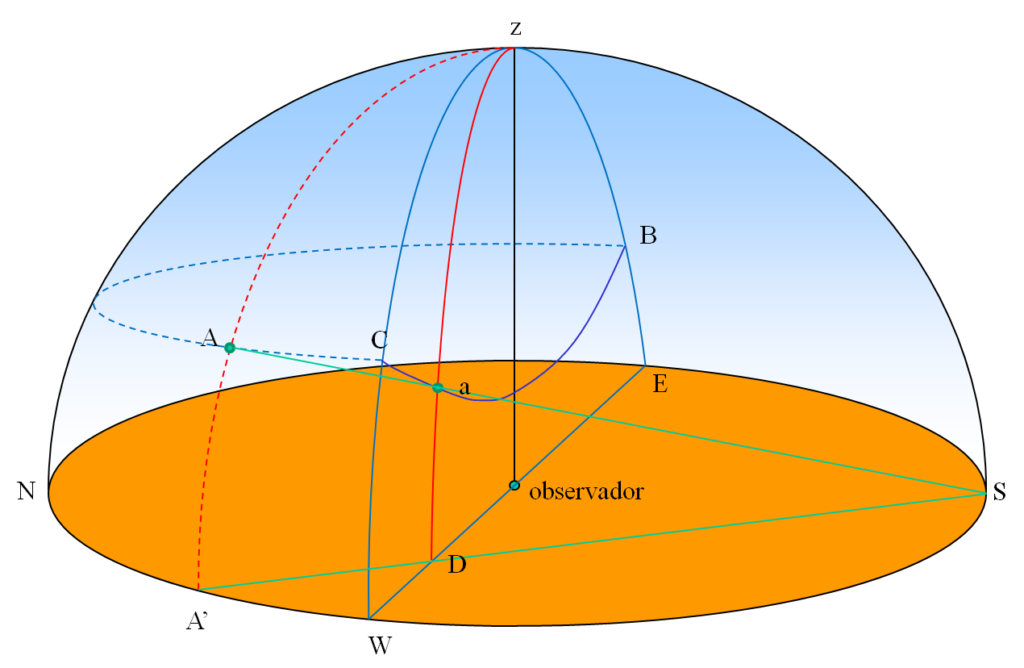
Ampliación: la proyección estereográficaPara el diseño de los semicírculos de visibilidad hemos utilizado una proyección estereográfica de centro el punto cardinal Sur (S) y plano de proyección en el primer vertical (EBzCW): el astro A de la esfera celeste se proyectará en el punto a del plano de proyección. El vertical de A (el cuarto de círculo zAA’) se convierte en el zaD y el almicántarat de A (BAC) en el arco BaC. Esta proyección tiene la enorme ventaja de que todas las circunferencias de la semiesfera celeste visible se convierten también en circunferencias, con lo que su trazado resulta relativamente sencillo.
|