Curso General de Astronomía
Tema 4. El modelo de las dos esferas
KEPLER. GRUPO DOCENTE DE ASTRONOMÍA
- Portada
- Presentación
- Tema 1. Geografía celeste
- Tema 2. Movimiento de rotación
- Tema 3. Coordenadas ecuatoriales
- Tema 4. El modelo de las dos esferas
- Tema 5. La Luna
- Tema 6. Las 4 estaciones
- Tema 7. Relojes de Sol
- Tema 8. Calendarios y eclipses
- Tema 9. Los Planetas. Cinemática
- Tema 10. El Sistema Solar.
- Tema 11. La Tierra y la vida
- Tema 12. Prismáticos y telescopios
- Tema 13. Una noche de observación
- Tema 14. Distancia a las estrellas
- Tema 15. Vida y muerte de las estrellas
- Tema 16. La Vía Láctea
- Tema 17. Galaxias
- Tema 18. Cosmología
- Anexo. Grandes astrónomos
- Bibliografía y Webs
4.2 El movimiento de rotación
En el tema anterior has realizado varias actividades que muestran en los semicírculos de visibilidad el movimiento aparente de las estrellas por la noche. Unas cuantas siempre están visibles y la mayoría salen y se ponen describiendo trayectorias más o menos parecidas a la del Sol si miramos hacia el Sur y circunferencias con centro en la estrella polar (que permanece fija) si lo hacemos hacia el Norte. Las figuras de las constelaciones son siempre las mismas, aunque pueden aparecer con diferentes orientaciones, según la fecha y la hora, y esas líneas imaginarias que nos llevan de una a otra en todo momento cumplen su función.
Da la impresión de que toda la esfera celeste en bloque gira alrededor del eje del mundo, en el sentido indicado por las flechas (figura 4.7), arrastrando a las estrellas (que parecen situadas, atornilladas, en ella) con la Tierra en reposo en el centro y por tanto el horizonte inmóvil (que es lo que nosotros vemos). Podemos imaginarnos una enorme esfera hecha de un material transparente pero sólido (al cielo también se le llama “firmamento”), algo así como cristal. De esta forma veremos a las estrellas salir por el Este y ponerse por el Oeste mientras que sus posiciones relativas permanecen inalterables.
Haz clic aquí para ver la animación 3
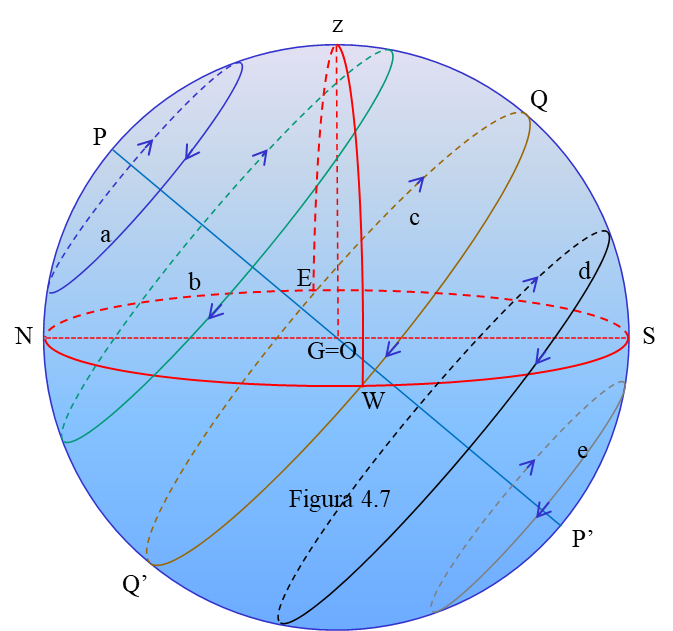
Una estrella como la a, situada a unos 30° del polo P (por tanto, estará a 60º del ecuador y su declinación será δ = 60º), realizará aparentemente un recorrido circular con centro en P y radio 30° siempre por encima del horizonte.
La estrella b que tiene una declinación de unos 30° saldrá por el NE y se pondrá por el NW; la parte más alta de su trayectoria se pasa al semicírculo sur.
Un astro (c) situado en el ecuador recorrerá precisamente esa línea, saliendo por el punto cardinal E, alcanzando una máxima altura de unos 50° sobre el S y poniéndose por el W.
Finalmente, d, con una declinación sur de unos 30°, tendrá un recorrido muy corto sobre el horizonte sur.
Todo esto es justamente lo que se observa:
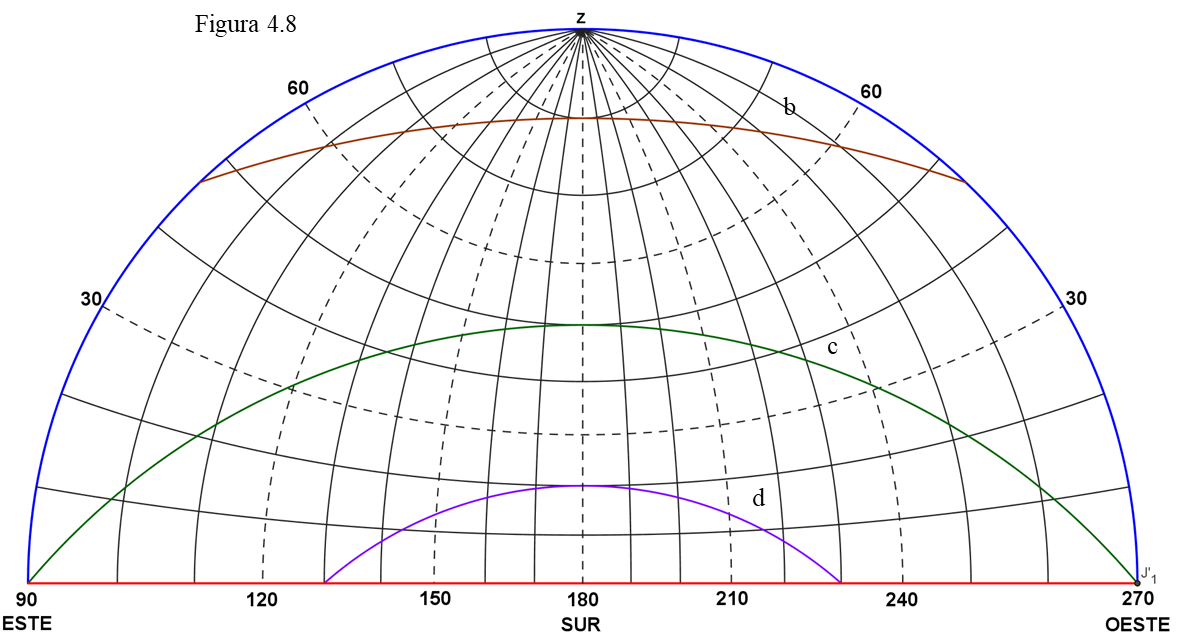
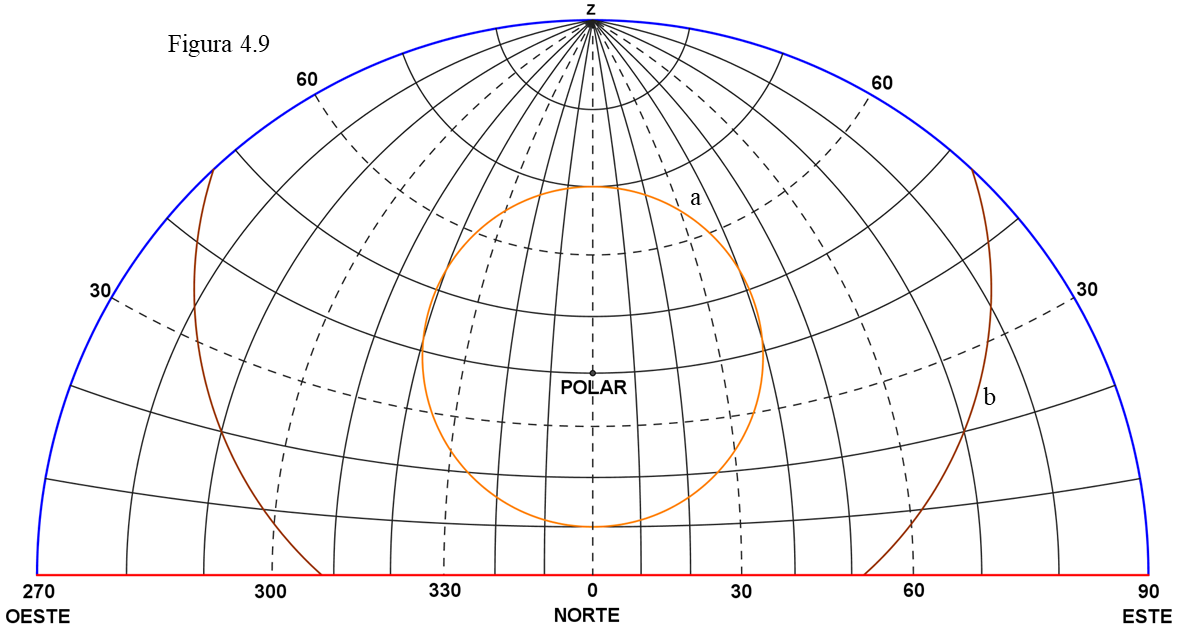
El camino descrito sobre nuestro horizonte por una estrella en particular viene determinado por su posición en la esfera celeste, más concretamente por su declinación, por su cercanía o lejanía al ecuador. Las estrellas con alta declinación estarán muy cerca de la Polar y las veremos recorrer un pequeño círculo a su alrededor, siempre mirando hacia el Norte y cruzarán dos veces el meridiano. En cambio, las que tengan declinación Sur, las que estén por debajo del ecuador, harán una trayectoria como el Sol de invierno, saliendo por el ESE, alcanzando una altura máxima en el meridiano relativamente pequeña y poniéndose por un punto simétrico, es decir por el WSW y serán visibles siempre mirando hacia el Sur. Algunas (como la b de los ejemplos anteriores) tienen una parte de su recorrido (la salida y la puesta) visibles en el semicírculo Norte y otra (la central) en el Sur.
Puedes comprobar con el planisferio que dos estrellas que tengan la misma declinación, como por ejemplo Capella y Deneb, ambas con una δ ≈ 45º, tienen el mismo acimut de salida y también la misma altura máxima meridiana: sus recorridos aparentes son idénticos, solo que lo recorren a diferentes horas.
Pero hay un pequeño detalle añadido, algo que no podemos observar pero que se deduce del modelo: tiene que haber estrellas, como la e, cuyo recorrido quede siempre invisible para nosotros. Ya desde tiempos muy antiguos se detectó que al viajar hacia el sur iban apareciendo constelaciones que antes no se podían ver. Desde nuestras latitudes nunca podemos ver Canopus (la segunda estrella más brillante del cielo), la Cruz del Sur, ni α Centauri, la más próxima.
Teniendo presente una imagen del modelo, como la de la figura 4.7, es muy fácil cuantificar algunos aspectos de los recorridos aparentes de las estrellas. Pero para hacerlo con comodidad en vez de esa imagen (figura 4.7) que pretende hacer ver las tres dimensiones de la esfera vamos a utilizar lo que llamamos la esfera celeste en sección que técnicamente es una proyección ortográfica (desde el infinito) sobre el plano del meridiano del lugar.
Ampliación: haz clic aquí para ver detalles
En la figura 4.10 de la página siguiente se ha representado la misma esfera celeste, pero sin perspectiva, sólo en sección. Los círculos (horizonte, ecuador, paralelos) se proyectan como segmentos de recta de forma que no podemos distinguir la mitad que está por delante de la que está por detrás. Aun así, podremos obtener de ella muchísima información.
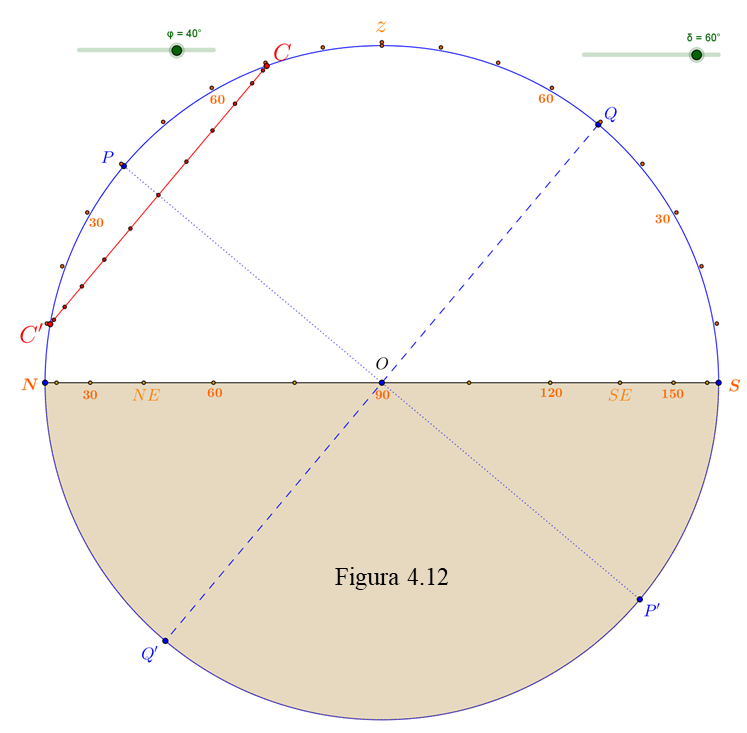
El círculo exterior (en azul) representa la esfera celeste, más concretamente el meridiano del lugar, con los dos polos P y P’, el cenit z y el ecuador QQ’. El diámetro horizontal NS es el horizonte en el que aparece la graduación (en naranja, de 15º en 15º) del acimut correspondiente a la parte de “atrás”, desde 0º en el Norte, pasando por 90º en el centro (donde se confunden los puntos cardinales E y W con el centro O) hasta 180º en el Sur. La graduación de la altura se señala (también en naranja) mediante puntos separados de 10 en 10 grados situados inmediatamente al exterior del círculo azul: tal y como estamos viendo la esfera celeste la altura de P es de 40° (desde N) y por tanto el punto más elevado del ecuador Q tendrá que estar a 50° de altura desde S.
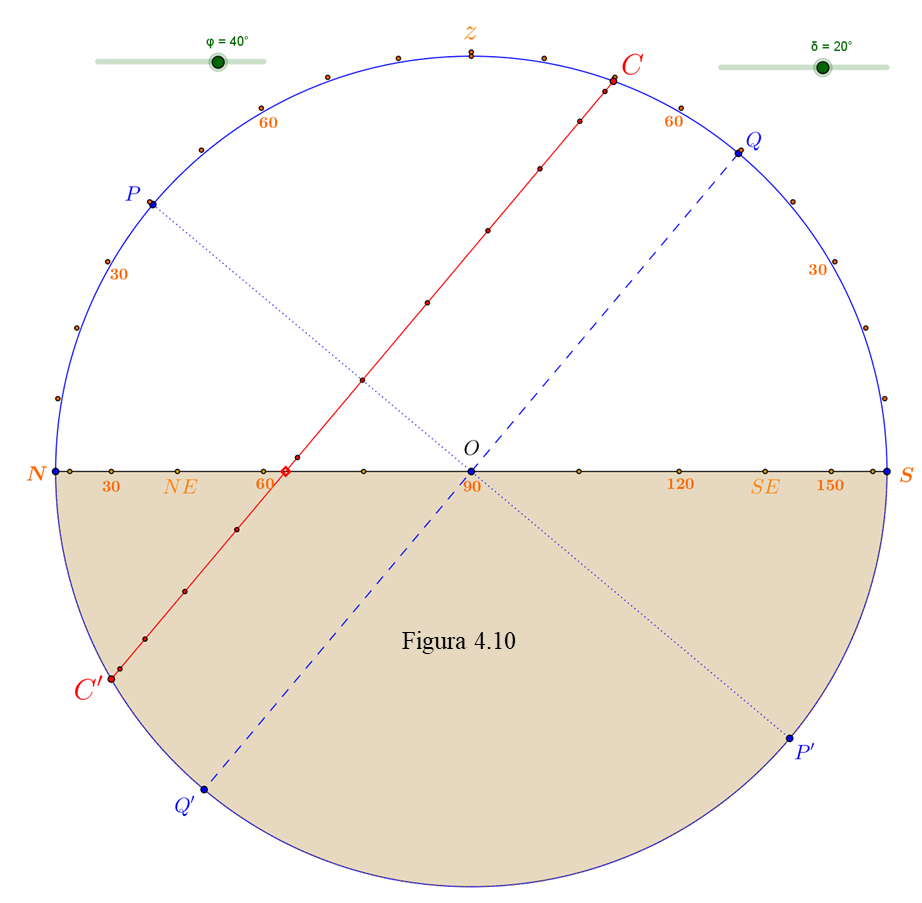
Consideremos una estrella de declinación δ = 20°. Recorrerá un paralelo situado 20° por encima del ecuador (el CC’, en rojo). Un pequeño rombo rojo señala el punto en el que CC’ corta al horizonte mostrando la posición del orto (o el ocaso) de esa estrella; vemos que su acimut de salida es de unos 63º aproximadamente (Este Noreste). También podemos observar que su máxima altura meridiana se alcanza en C y es de 70º. Puedes comprobar estos resultados con el planisferio: una estrella brillante de declinación 20º es Arturo (en realidad tiene una δ = 19°, con lo que habrá mínimas diferencias).
Más todavía: el paralelo CC’ está dividido mediante pequeños puntos rojos en 12 tramos, cada uno correspondiente a una hora de tiempo. Desde C hasta el eje PP’ hay 6 horas y desde el eje hasta C’ otras 6. ¿Cuántos tramos (horas) quedan por encima del horizonte? Contemos: desde C hasta el eje PP’ hay 6 y entre el eje y el orto hay algo más de una hora, digamos aproximadamente 1 h 15 m. En total 7 h 15 m. Este es el tiempo que transcurre desde que esa estrella sale hasta que llega a su culminación en C. Otro tanto pasará desde C hasta su puesta, así que una estrella de δ = 20º está por encima de nuestro horizonte 14 h 30 m. Otra cosa es que se vea todo ese tiempo pues eso dependerá de si el sol está presente ocultándola con su luz o si es de noche. También puedes utilizar el planisferio y la estrella Arturo para verificar, aproximadamente, este resultado teórico.
En cambio, un astro de declinación 60° (como δ Cas) describirá un paralelo siempre por encima del horizonte; será una estrella circumpolar que cruzará el meridiano dos veces, en su culminación superior (C) llegará a tener una altura de 70° y en la inferior (C’) sólo se elevará 10° por encima del punto cardinal Norte.
Compruébalo con el planisferio y con δ Cas.
Así pues, como ya hemos indicado antes, la trayectoria aparente de una estrella concreta depende exclusivamente de su declinación.
Ejercicio 4.1
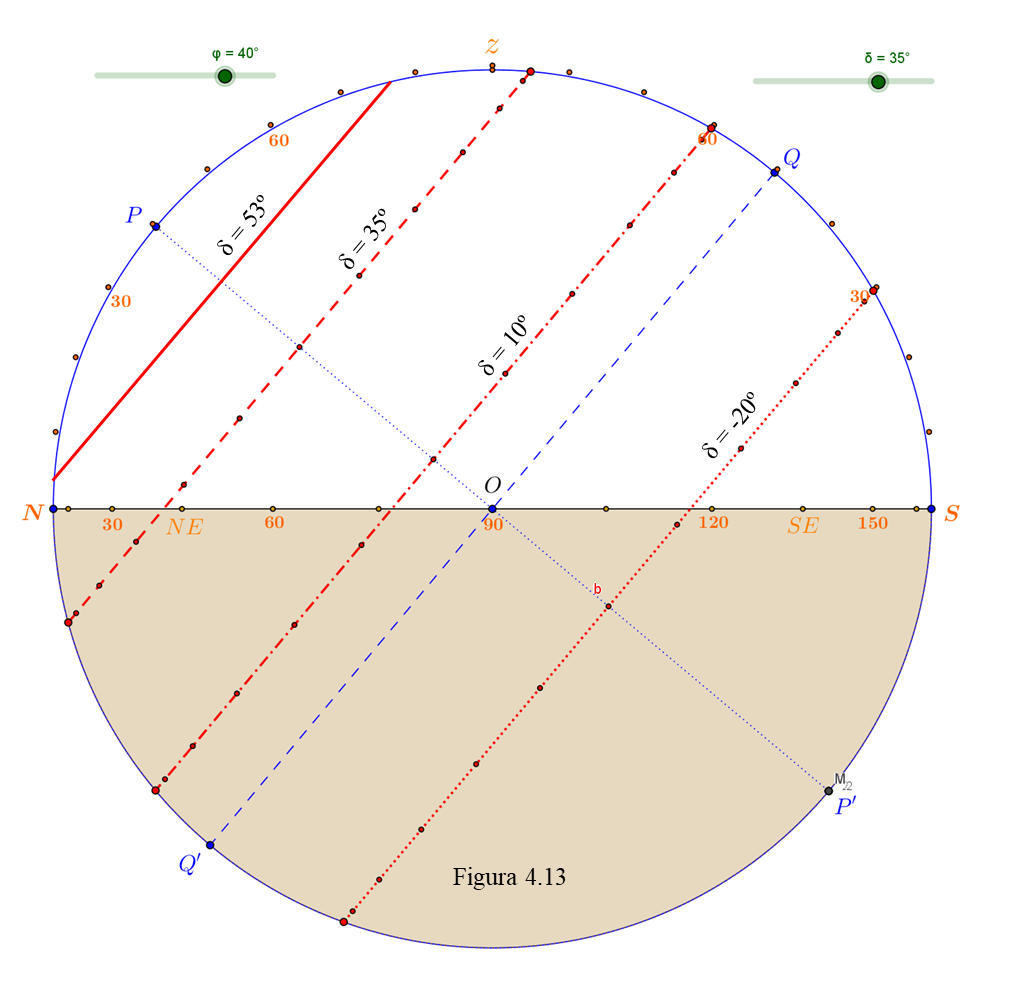
Completa esta tabla (algunas celdas quedarán en blanco):
| Declinación | -20° | 10° | 35° | 53° |
| Acimut Orto | ||||
| Máxima altura | ||||
| Acimut Ocaso | ||||
| Culminación inf. | ||||
| Culminación sup. | ||||
| Horas por encima del horizonte |
 Haz clic aquí para ver la solución
Haz clic aquí para ver la solución
Ejercicio 4.2
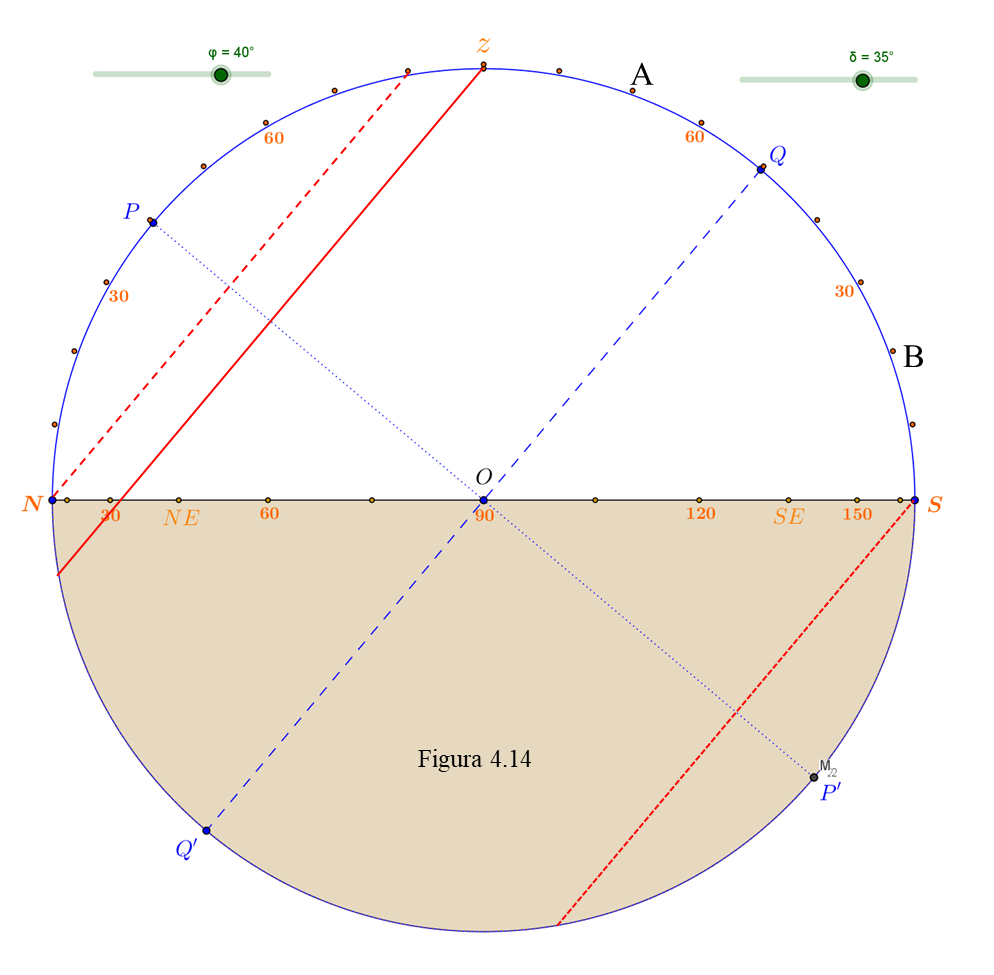
En estos dibujos en sección, la declinación de un paralelo se puede calcular midiendo la distancia hasta el ecuador, hasta Q. Por ejemplo, el punto A está 20º “por encima” (al Norte) de Q, mientras que B tiene una declinación de -30º.
- ¿Cuál es la declinación límite para que una estrella sea circumpolar (siempre visible)?
- ¿Cuál debe ser la declinación de una estrella para que pase por el cenit?
- ¿Cuál es la declinación límite para que una estrella no se vea nunca?
 Haz clic aquí para ver la solución
Haz clic aquí para ver la solución