Curso General de Astronomía

Tema 4. El modelo de las dos esferas

KEPLER. GRUPO DOCENTE DE ASTRONOMÍA

4.6 Trabajos escolares

Esfera armilar


La esfera armilar es un modelo en tres dimensiones de la esfera celeste. Recibe su nombre de la palabra latina armilla que significa aro o anillo. Cada uno de ellos representa alguno de los elementos astronómicos más significativos: eclíptica, ecuador celeste, horizonte, meridiano… Durante siglos fue utilizado como un excelente modelo para calcular diversas magnitudes astronómicas y para la predicción de otras.

La construcción y/o uso de una esfera armilar en el ámbito escolar (figura 4.29) se convierte en una excelente herramienta didáctica que puede competir con conocidos programas informáticos.

Si se dispone de una esfera celeste sólida y que pueda girar alrededor de su eje, se puede realizar un modelo físico tangible del universo de las dos esferas. Hay que inclinar la esfera celeste hasta que el eje tenga la orientación adecuada y construir con madera fina, cartón o similar una banda que simule el horizonte. Se pueden así visualizar mejor todas estas actividades.

CONSTRUCCIÓN

Para simplificar su fabricación partiremos de una esfera celeste a la que añadiremos un horizonte externo de forma parecida a la que se observa en la figura 4.30 de este detalle del cuadro “El astrónomo” de Johannes Vermeer.

El resultado podéis verlo en la figura 4.31, una esfera celeste con horizonte transformada en armilar en el Aula de Astronomía de Fuenlabrada.

Utilizaremos para ello, una esfera de 30 cms. de diámetro de la marca scanglobe (figura 4.32) en la que se recogen las constelaciones (que aparecen al revés de cómo las vemos en el cielo ya que las miramos desde “fuera”) y los elementos celestes más representativos.

Para la fabricación seguiremos los siguientes pasos:

  1. Quitamos la peana que soporta la esfera y retiramos el sistema eléctrico.
  2. Fabricamos el meridiano.
Unimos el semimeridiano (figura 4.33) con otro arco metálico idéntico de otra esfera scanglobe (no tiene por qué ser celeste ya que los globos terráqueos que se utilizan en los centros escolares utilizan el mismo) o bien cortamos un arco de contrachapado con las mismas dimensiones que el metálico y los unimos entre sí. Después, con las piezas propias de la esfera la unimos al meridiano (figura 4.34).  
  1. Fabricamos el horizonte

Cortamos un arco de cartón pluma o contrachapado (figura 4.35) de unos 31 cm de diámetro y unos 5 de ancho que encajaremos en una cruceta (figura 4.36). También Podemos cortar un círculo de las dimensiones descritas en el tablero de una mesa camilla (figura 4.37). Graduamos el horizonte, bien en azimut de 0 a 360º o en 180º a partir del Este y Oeste si queremos estudiar los puntos de salida y puesta de estrellas y el Sol sobre esos puntos. Realizamos una ranura sobre el Norte y otra en el Sur para encajar el meridiano.

POSICIONAMIENTO DE LA ESFERA

La observación de la esfera celeste depende de la latitud en la que nos encontremos. Por ello deberemos colocar el eje del mundo, que está orientado a la polar, sobre el horizonte norte con una inclinación igual a la latitud.

 

Si el meridiano lo hemos fabricado a partir de dos semimeridianos engarzados, hay que tener en cuenta que la graduación que presentan sitúa el polo norte a 90º. Para orientar la esfera en una latitud de 40º, por ejemplo, hay que situar la polar a 40º sobre el horizonte Norte. La graduación que leeremos en el meridiano desde el horizonte ha de ser, por tanto, de 50º.

APLICACIONES DIDÁCTICAS

Además del estudio de elementos visibles en una esfera celeste convencional (eje del mundo, meridianos y paralelos celestes, eclíptica, círculo horario, coordenadas, zodíaco), la esfera armilar nos permite determinar y calcular diversos parámetros. Entre ellos, los más importantes son:

  1. La posición del Sol en el cielo. En la esfera tenemos señaladas las posiciones del Sol cada diez días (puntos rojos con fecha anotada debajo de ellos). Seleccionamos, con una pegatina (figura 4.39), la posición del Sol en la fecha que se quiera estudiar.

Con ella podemos predecir

  1. Su altura al mediodía. Situamos el Sol bajo el meridiano. Leemos la altura que alcanza desde el horizonte. En ese momento serán las 12’00 horas en T.U. Giramos el círculo horario para que marque las 12’00 bajo el meridiano (figura 4.40).
  1. Hora y acimut de salida. Giramos la esfera hasta que el Sol se sitúe saliendo por el Este. Leemos el acimut en el horizonte y la hora de salida en el círculo horario (figura 4.41).
  2. Hora y acimut de puesta. Giramos la esfera hasta que el Sol se ponga por el Oeste. Leemos el acimut y la hora de puesta.
  3. Duración del día.
  1. Orto, culminación y puesta de las estrellas. Constelaciones circumpolares

  2. El Sol en los cambios estacionales

  3. El cielo en otras latitudes
    1. En el Polo Norte. Circumpolaridad de todas las estrellas. El día perpetuo en el verano. La noche perpetua en el invierno.
    2. En el Ecuador. Todas las estrellas son estacionales. Describen círculos perpendiculares al horizonte. Estudio de las trayectorias del Sol.
    3. En los círculos polares. El Sol de medianoche.
    4. En los trópicos. El Sol cenital.

La medida del tamaño de la Tierra (por Eratóstenes)

Eratóstenes fue un astrónomo, matemático y geógrafo griego que vivió entre los años 275 y 195 a.C. Su contribución más importante y conocida fue la medición de la circunferencia terrestre, recogida en la obra de Cleomedes Sobre los movimientos circulares de los cuerpos celestes. Parte de los siguientes datos:

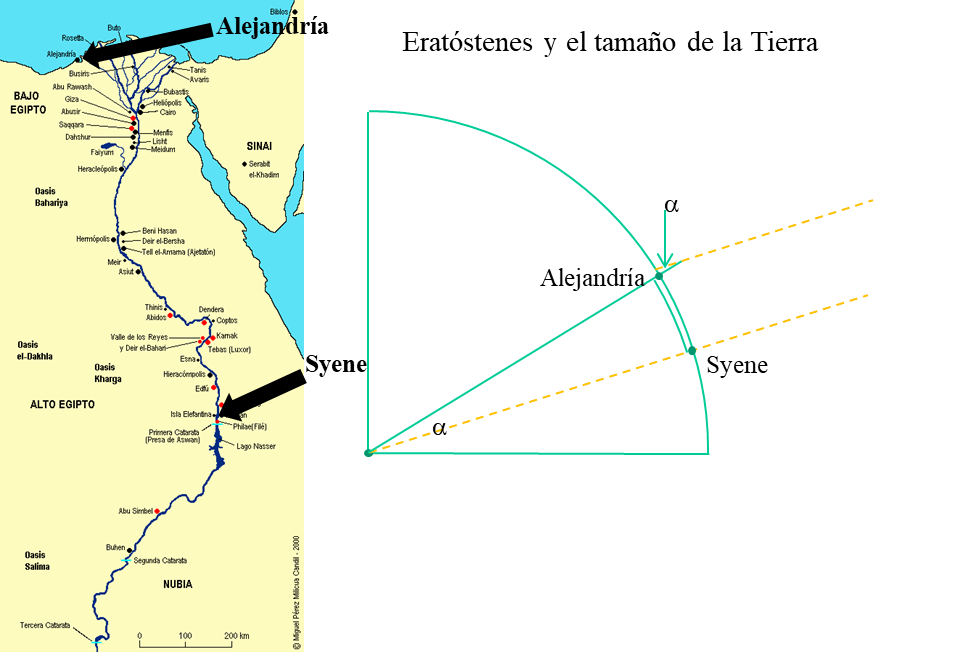
  • En la ciudad de Syene (cerca de la actual Asuán, en el Alto Egipto) los rayos del sol inciden verticales el día del solsticio de verano.
  • Ese mismo día, en Alejandría los rayos del sol forman con la vertical un ángulo de 1/50 de circunferencia.
  • Alejandría y Syene están en el mismo meridiano y su distancia es de 5.000 estadios.
  • En consecuencia, la longitud de la circunferencia terrestre es de 50·5.000 = 250.000 estadios.

Son evidentes dos cuestiones:

  1. El método es impecable.
  2. Eratóstenes no podía confiar en la precisión de ninguna de las medidas utilizadas para hacer esa estimación. De hecho, Alejandría y Syene no están en el mismo meridiano, sino que distan 3° en longitud. La diferencia en latitud real es de 7° 7′, casi exactamente igual a la determinada por Eratóstenes (1/50 de 360° = 7° 12′, es decir, un error de sólo 5′ de arco).

Los dos primeros datos (los ángulos) serían determinados seguramente mediante el gnomon, mientras que para la distancia entre Alejandría y Syene, se fió de las estimaciones oficiales, realizadas por los bematistas o “contadores de pasos”.

Por otra parte, sigue existiendo gran controversia acerca de la medida del estadio utilizado por Eratóstenes. La asignación más frecuente es 1 estadio = 157,5 metros, con lo que resulta para la circunferencia terrestre una longitud de 250.000·57,5 = 39.375 Km, un resultado asombrosamente preciso.

Este cálculo puede realizarse escolarmente mediante la medida simultánea de la altura del Sol en dos centros escolares situados en el mismo meridiano y lo más alejados posibles. La medición puede realizarse con un gnomon y la distancia entre ambas ciudades puede obtenerse de cualquier mapa.

<<
>>
Scroll Up