5.7 La Luna como satélite.
La órbita de la Luna alrededor de la Tierra es una elipse de pequeña excentricidad (0,055) por lo que su distancia no es constante, pudiendo variar hasta un 14%.
| Mínima | Media | Máxima |
| perigeo | apogeo | |
| 356.400 km | 384.400 km | 406.700 km |
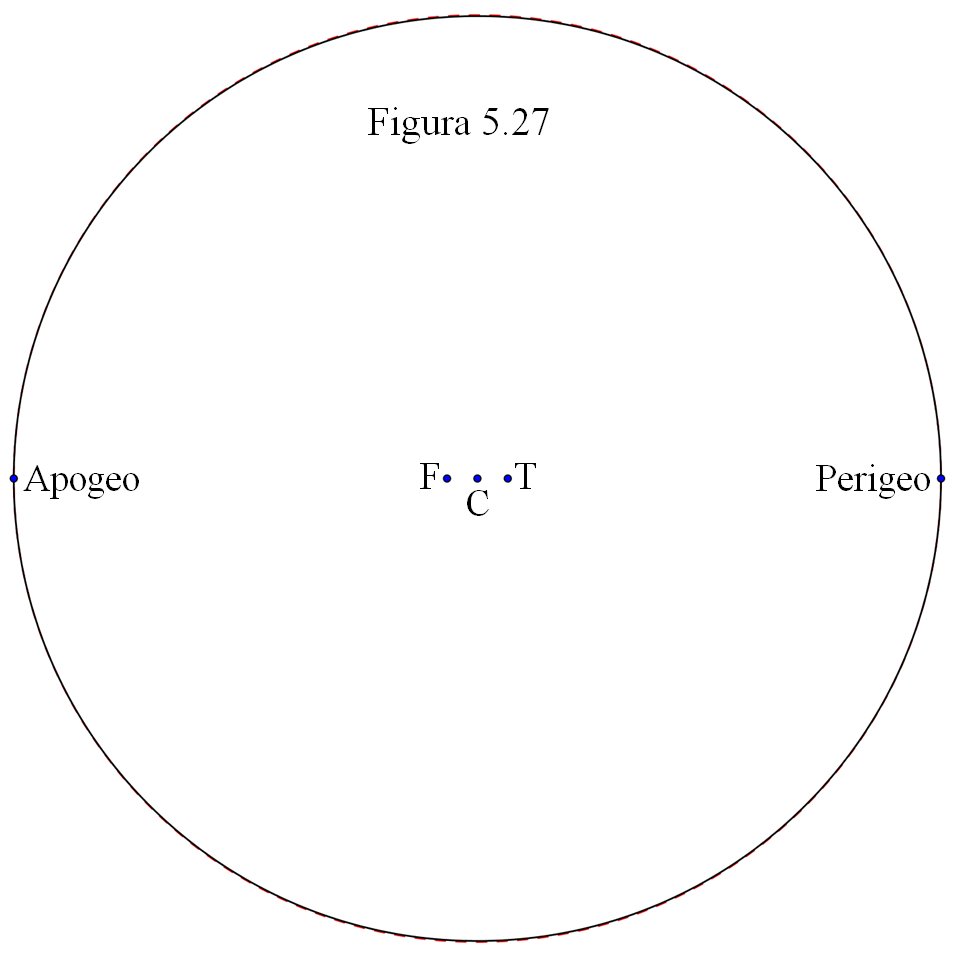
La Tierra ocupa uno de los focos de la elipse, siendo el otro el punto F; C es el centro de la órbita. Aparece también dibujada (en rojo discontinuo) una circunferencia de centro C y radio la distancia media entre la Tierra y la Luna. Apenas es posible distinguirla de la elipse (dibujada en negro). Sin embar- go, sí que se aprecia la posición excéntrica de la Tierra que es la causa de esa variación en la distancia y que tiene como consecuencia que el tamaño aparente de nuestro satélite sí varíe algo, aunque no es fácil apreciarlo a simple vista. En la figura 5.28 se muestra ese cambio.
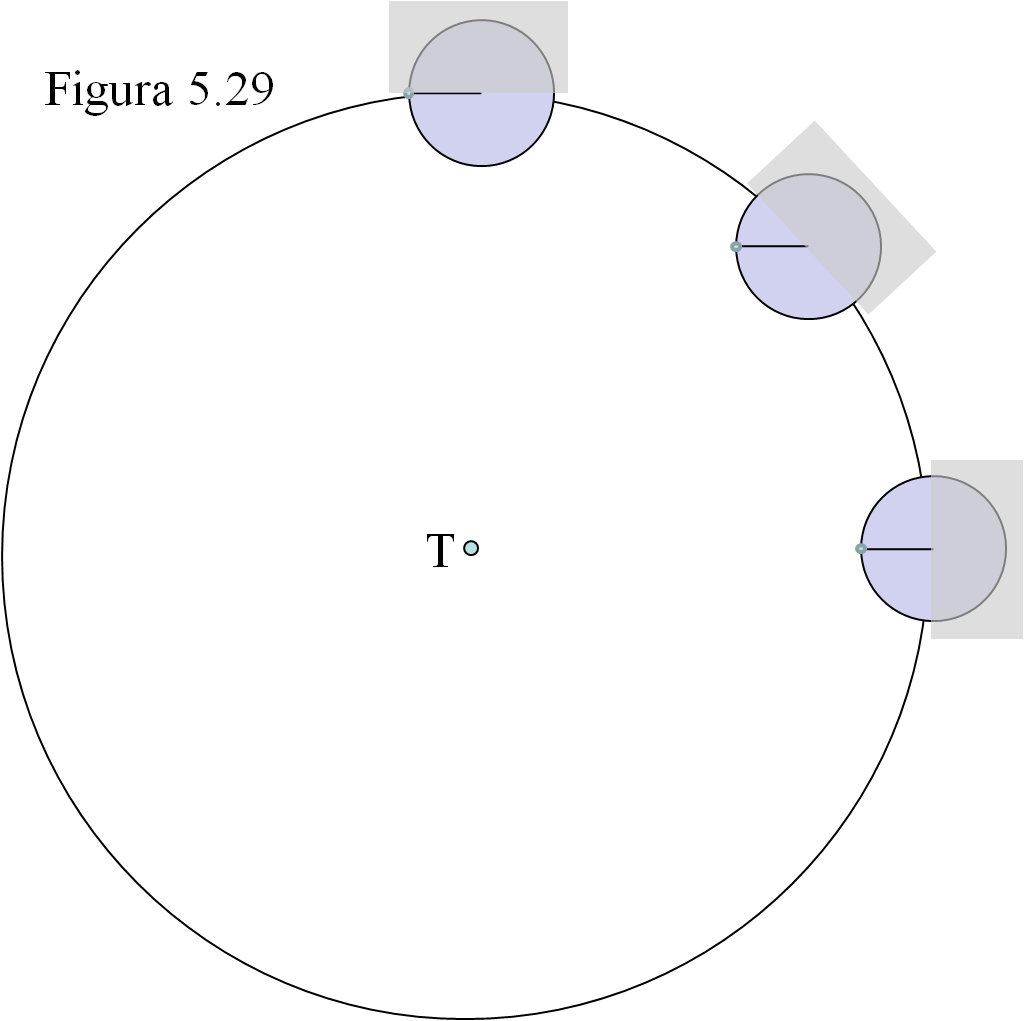
Nuestro satélite siempre presenta hacia la Tierra la misma “cara”, siempre vemos los mismos accidentes (mares y cráteres) en la misma posición. El mare Serenita- tis, por ejemplo, está permanentemente un poco a la derecha del centro y a medio camino entre el ecuador y el polo Norte. Esto, que puede parecernos lo más normal del mundo, no lo es en absoluto. Puesto que la Luna va avanzando por su órbita, un detalle cualquiera de su superficie debería irse desplazando como se indica en la figura 5.29.
¿Qué es lo que tiene que suceder para que ese punto permanezca enfrentado a T?
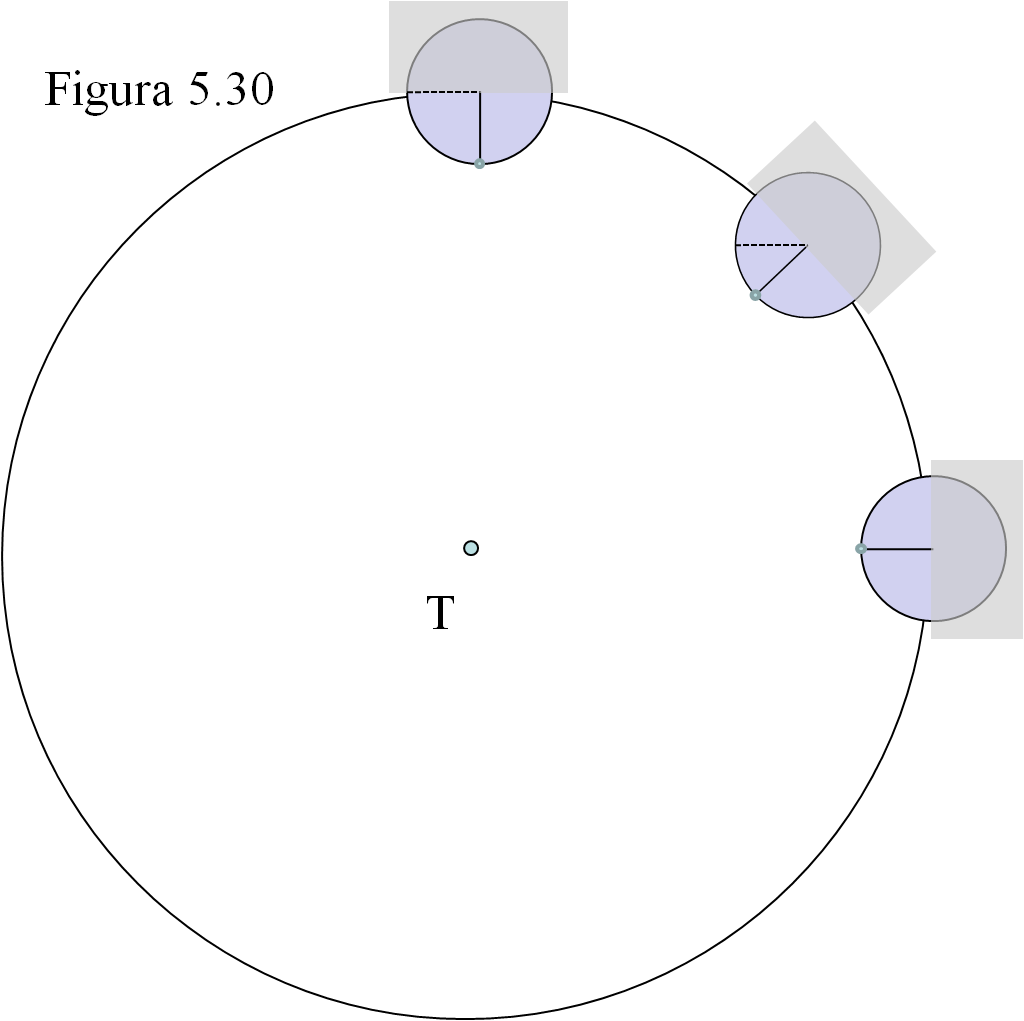
Pues debe ocurrir lo que ilustra la figura 5.30: la Luna rota sobre sí misma exactamente al mismo ritmo que avanza por su órbita. Cuando ha recorrido 40º es preciso que gire sobre su eje los mismos 40º y en el mismo sentido (antihorario) para que ese punto siga estando mirándonos de frente y no se vaya desplazando hacia la izquierda como ocurriría (figura 5.29) si no hubiera rotación.
Este acoplamiento entre traslación y rotación es bastante frecuente entre los satélites y recibe el nombre de rotación sincrónica.
En realidad, pequeñas perturbaciones en los movimientos lunares (que son los más complicados de estudiar y predecir, los que requieren teorías más complejas) hacen que nuestro satélite se bambolee un poco y podamos llegar a ver algo más de la mitad (en torno al 58%) de su superficie.
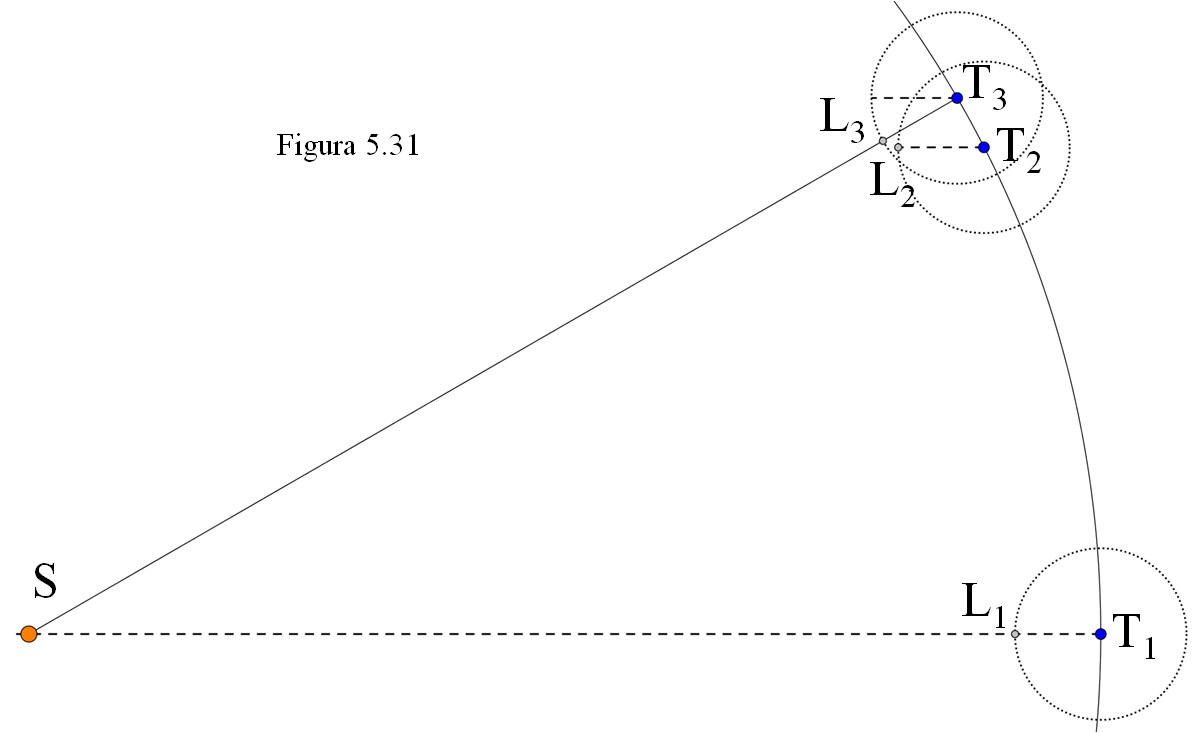La traslación de la Luna alrededor de la Tierra no se completa en 29,53 días, sino en un tiempo algo menor (27,3 días) periodo bautizado como mes sidéreo. Esta diferencia se debe al movimiento orbital de nuestro planeta en torno al Sol.
Si comenzamos en una luna nueva (posición T1 L1), cuando se complete una vuelta el radio T2L2 quedará paralelo al T1L1, pero como la Tierra ha avanzado desde T1 hasta T2, entonces la dirección T2L2 no apunta hacia el Sol y no estaremos aún en la siguiente luna nueva. Para alcanzarla tendremos que esperar un par de días hasta que lleguemos a la posición T3L3.
Todas las líneas discontinuas T1L1, T2L2 y el segmento paralelo a ellas que parte de T3 se dirigen desde la Tierra hacia un mismo punto de la infinitamente lejana esfera celeste, hacia una misma estrella. Por eso el tiempo que trascurre desde que la Luna se sitúa entre la Tierra y una estrella determinada, hasta que se repite la misma situación recibe el nombre de mes sidéreo (relativo a las estrellas).
En cambio, el mes por antonomasia, el periodo entre dos lunas nuevas consecutivas, que es el tiempo que trascurre desde que la Luna está entre la Tierra y el Sol hasta que vuelve a producirse esa misma disposición se llama mes sinódico (de sínodo: reunión, en este caso hablamos de la “reunión”, vistos desde la Tierra, de la Luna y el Sol).
Distancia y tamaño
Sabemos que la Luna está más cerca de la Tierra que el Sol porque en los eclipses se interpone entre nosotros y nuestra estrella. Además, si estuviera más lejos no veríamos las fases como lo hacemos, sino que estaría siempre llena o casi llena. Otro efecto de su cercanía es el de las ocultaciones de estrellas o de planetas que suceden cuando el satélite pasa por delante de un astro impidiendo que su luz llegue hasta nosotros.
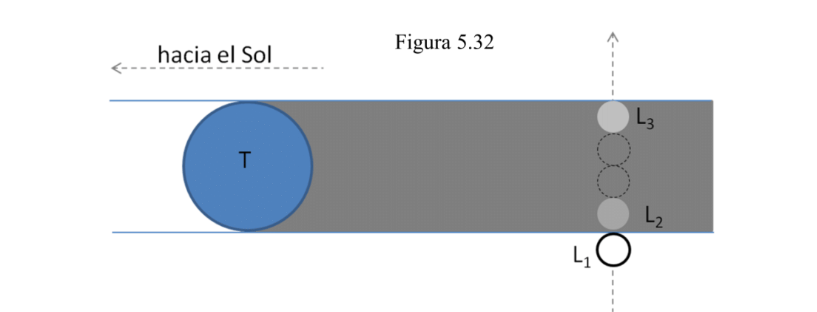
Los primeros cálculos fueron realizados por los grandes astrónomos griegos Aristarco, Hiparco y Ptolomeo (entre los siglos –III y II). Para averiguar el tamaño de la Luna pensemos en un eclipse total de nuestro satélite. La sombra producida por la Tierra es un cono pero, dada la lejanía del Sol, podemos suponer que es un cilindro y medir (figura 5.32) el tiempo que transcurre desde L1 (momento en que la Luna comienza a entrar en la sombra) a L2 (cuando ya toda ella queda oculta) y a L3 (instante en el que reaparece). Se encontró que el tiempo en ir de L1 a L3 era 4 veces el de L1 a L2. Eso quería decir que en la sombra proyectada “entran” aproximadamente 4 lunas, con lo que DL = ¼ DT = 0,25 · DT. Es una estimación aceptable puesto que la proporción real es DL = 0,27 · DT. Ahora sabemos que DT = 12.742 km, por lo que la estimación obtenida es DL = 3.185,5 km frente al dato correcto que es DL = 3.474 km.
Para hallar la distancia Tierra-Luna los astrónomos griegos utilizaron varios razona- mientos. El más sencillo se basa en la figura 5.33. Ya conocemos que DL = 0,25·DT y queremos averiguar la distancia TL. Como la Luna abarca un ángulo de 31’, en toda la circunferencia de su órbita “caben” 360º·60’/31’ = 697 lunas, luego esa circun- ferencia medirá 697·DL = 697·0,25·DT y su radio TL = 697·0,25·DT / 2 π = 27,7·DT (la distancia media real es de 30,16·DT). En términos absolutos la estimación (sabiendo que DT = 12.742 km) fue TL = 353.000 km frente a un valor exacto de 384.400 km.
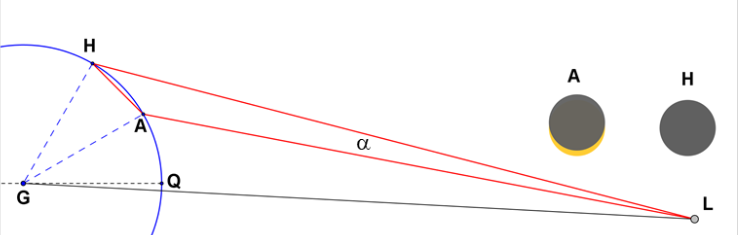
Ampliación: la distancia Tierra – LunaHiparco utilizó ingeniosamente los datos de un eclipse solar (el del 14 de marzo de -189) que fue total en Hellesponto (a unos 40º de latitud) pero solo parcial de magnitud 4/5 en Alejandría. Eso le permitió estimar el ángulo α de la figura y, a base de reiterados cálculos trigonométricos llegó a la conclusión de que TL = 30,5·DT, un valor muy preciso.
Pero los eclipses de Sol son visibles muy raras veces. Mucho después (a partir del siglo XVIII), cuando hubo instrumentos adecuados para medir ángulos con gran exactitud se pudo utilizar un procedimiento similar sin necesidad de esperar a que hubiera un eclipse solar. La figura muestra el instante en que la Luna (L) pasa por el meridiano de dos lugares distintos de la superficie terrestre (A y B). Tienen que tener la misma longitud y debemos conocer su latitud, así como el radio de nuestro planeta. Las únicas observaciones necesarias son las alturas de la Luna sobre el horizonte en ese momento en A y en B. Armados con tan poca artillería el procedimiento a seguir es ir resolviendo un triángulo tras otro hasta alcanzar nuestro objetivo final: determinar la distancia GL.
Recientemente se utiliza el reflejo (en espejos colocados en la Luna) de un rayo láser lanzado desde la Tierra con lo que se obtienen medidas de una precisión extraordinaria (del orden del cm). |
