- Portada
- Presentación
- Tema 1. Geografía celeste
- Tema 2. Movimiento de rotación
- Tema 3. Coordenadas ecuatoriales
- Tema 4. El modelo de las dos esferas
- Tema 5. La Luna
- Tema 6. Las 4 estaciones
- Tema 7. Relojes de Sol
- Tema 8. Calendarios y eclipses
- Tema 9. Los Planetas. Cinemática
- Tema 10. El Sistema Solar.
- Tema 11. La Tierra y la vida
- Tema 12. Prismáticos y telescopios
- Tema 13. Una noche de observación
- Tema 14. Distancia a las estrellas
- Tema 15. Vida y muerte de las estrellas
- Tema 16. La Vía Láctea
- Tema 17. Galaxias
- Tema 18. Cosmología
- Anexo. Grandes astrónomos
- Bibliografía y Webs
6.2 Las explicaciones
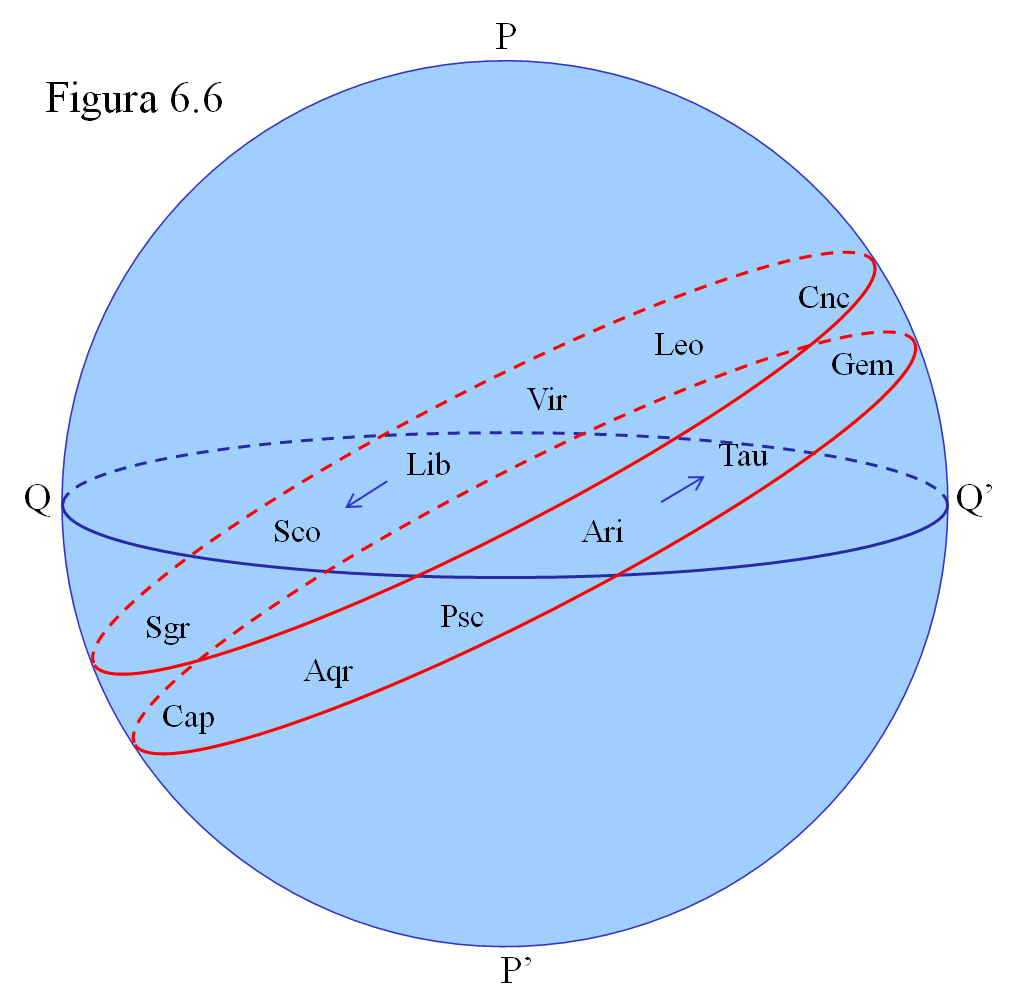
Hasta aquí hemos recogido y sistematizado muchas observaciones que ponen de manifiesto la existencia de un ciclo solar. Es el momento de encontrar una explicación sencilla de todas ellas, un marco teórico que permita hacer frente a todo lo que hemos ido recopilando.
Visto desde la Tierra, el Sol se mueve a lo largo del año pasando por delante de las doce constelaciones del Zodíaco: Aries, Tauro, Geminis, Cancer, Leo, Virgo, Libra, Escorpio, Sagitario, Capricornio, Acuario y Piscis. El Zodíaco forma como una banda, como un cinturón, que está inclinado con respecto al ecuador celeste.
Al moverse el Sol lentamente siguiendo el orden de las constelaciones zodiacales, su declinación va cambiando. Desde Aries hasta Virgo está por encima del ecuador y tiene declinación positiva o norte. Desde Libra hasta Piscis, en cambio, queda por debajo del ecuador.
Con más precisión la trayectoria aparente del Sol a lo largo del año respecto a las estrellas es la línea central del Zodíaco, que se llama eclíptica. Los puntos en los que corta al ecuador corresponden a los días en los que tiene δ = 0o y son los equinoccios. Los días en los que el Sol alcanza su declinación extrema (δ = ± 23,5o) corresponden a los solsticios. Así, el ciclo anual queda dividido en cuatro etapas naturales:
PRIMAVERA, desde el equinoccio de primavera (EqP, 21 marzo) al solsticio de verano (V, 22 junio)
VERANO, desde el solsticio de verano al equinoccio de otoño (EqO, 22 septiembre)
OTOÑO, desde el equinoccio de otoño al solsticio de invierno (I, 22 diciembre)
INVIERNO, desde el solsticio de invierno al equinoccio de primavera.
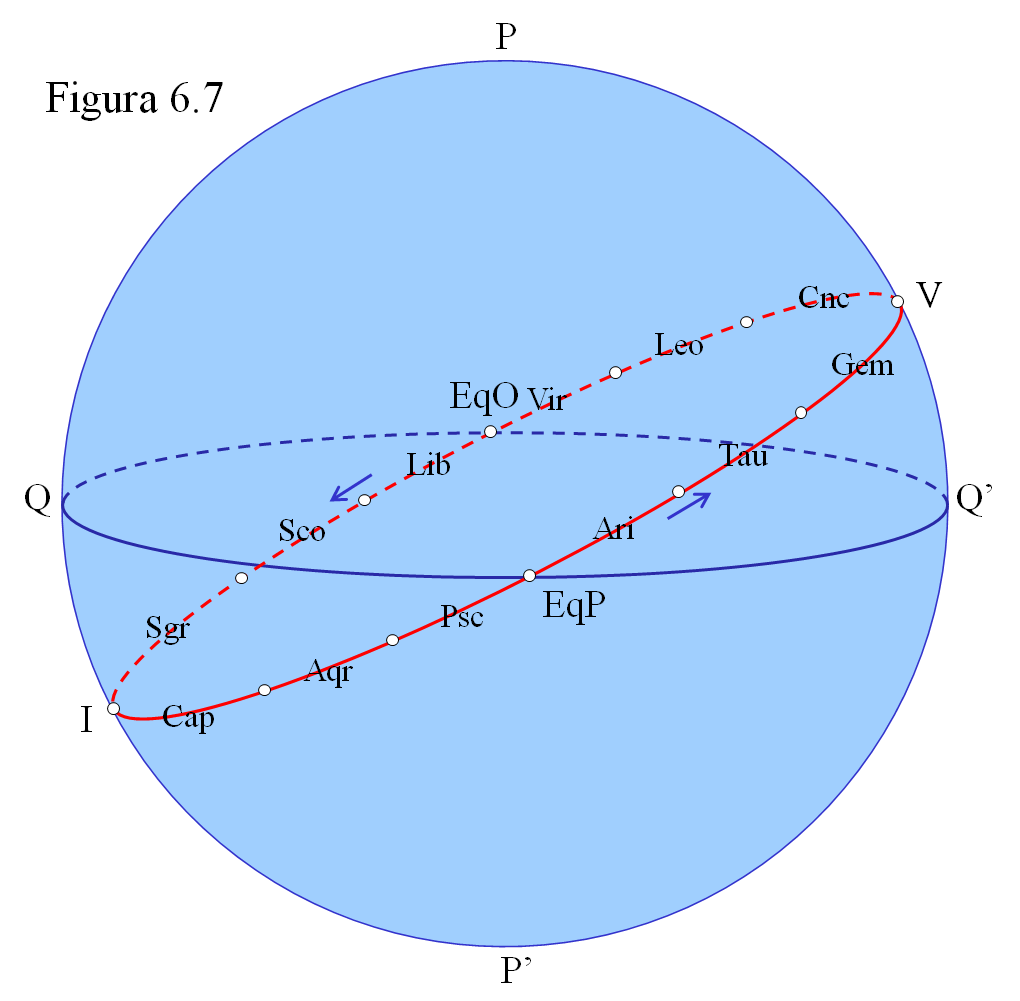
Uno de los puntos en los que la eclíptica corta al ecuador, el correspondiente al equinoccio de primavera, es el que se toma como origen para la medida de la ascensión recta. El meridiano 0 es, por convenio, el que pasa por el equinoccio de primavera.
Durante un día cualquiera el recorrido aparente del Sol por encima del horizonte, desde que sale hasta que se pone, es el normal de cualquier estrella, arrastrado por el movimiento general aparente de la esfera celeste de Este a Oeste en 24 horas. El Sol describirá cada día el paralelo celeste que le corresponda según la declinación que tenga en esa fecha.
En la figura 6.8 se representan las trayectorias diurnas del Sol, vistas desde un lugar situado a unos 40o de latitud Norte, en diferentes épocas. En los dos equinoccios, cuando la δ del Sol es de 0o, éste recorrerá el ecuador, es decir, saldrá por el Este y se pondrá por el Oeste.
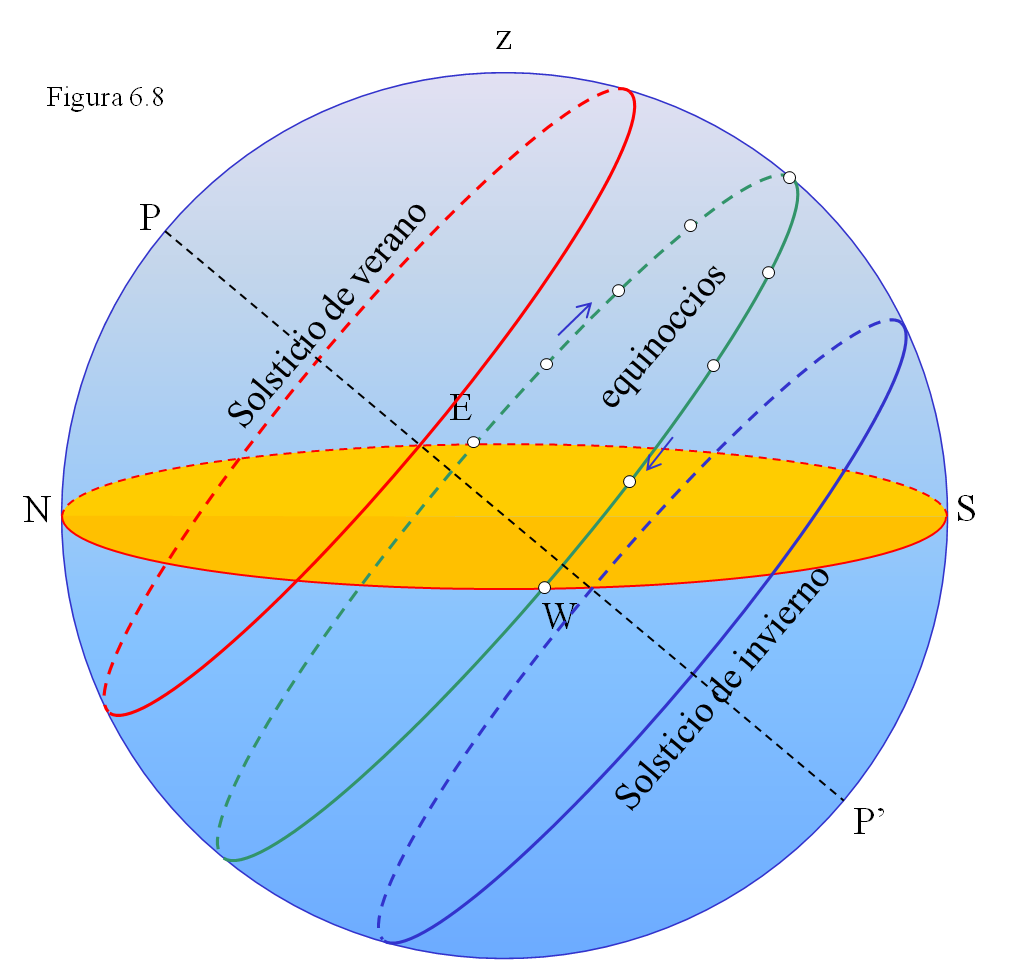
En el solsticio de verano su declinación es δ = +23’5o y durante el día 22 de junio recorrerá ese paralelo, por lo que no saldrá por el Este, sino bastante hacia el Norte y también se pondrá por un punto del horizonte noroeste. El día es muy largo y el Sol, a mediodía, cuando pasa por el meridiano, está muy alto, cerca del cenit. Estará calentando mucho la superficie terrestre.
En el solsticio de invierno (δ = -23’5o) ocurre exactamente lo contrario: sale por el sureste y se pone hacia el suroeste, el día es muy corto y la noche larga. El astro rey alcanza muy poca altura a mediodía y calienta mucho menos.
En los equinoccios la situación es intermedia.
En la figura 6.9 se ha representado la misma esfera celeste pero sin perspectiva, sólo en sección como hicimos en el tema 4. Los círculos (horizonte, ecuador) se proyectan como segmentos de recta de forma que no podemos distinguir la mitad que está por delante de la que está por detrás. Aún así podremos obtener de ella muchísima información.
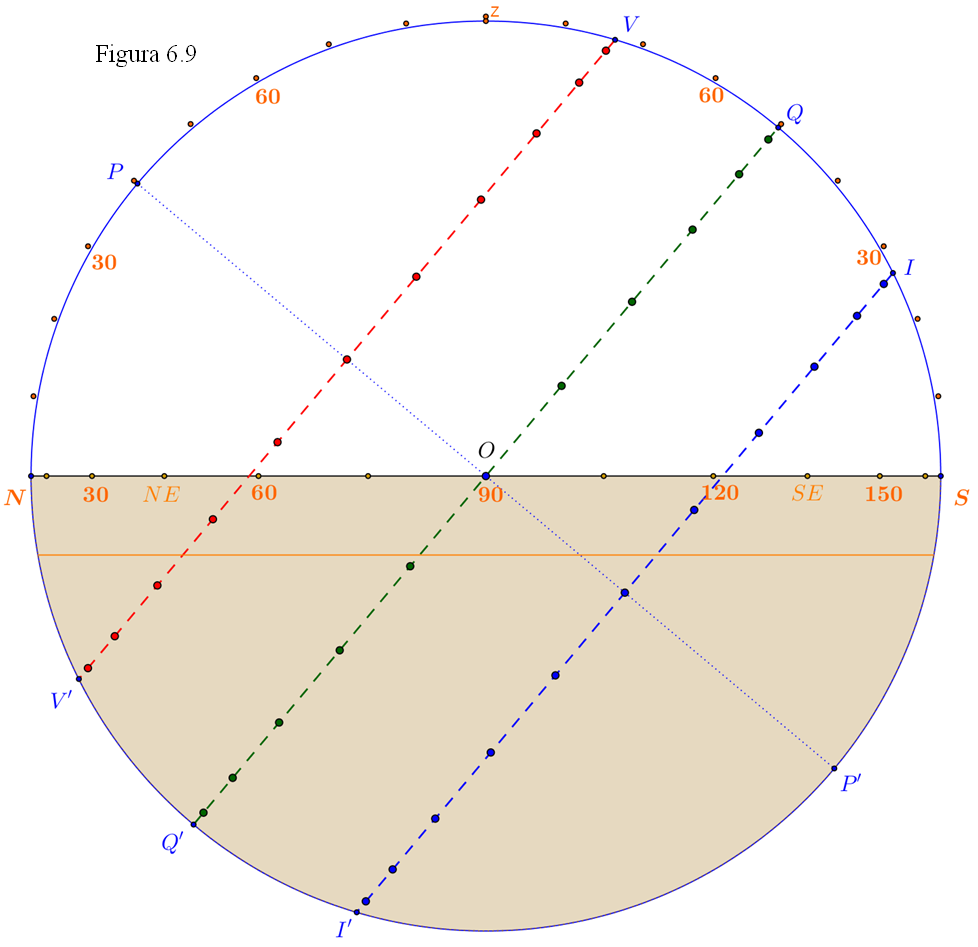
La circunferencia exterior (en azul) representa la esfera celeste, más concretamente el meridiano del lugar, con los dos polos P y P’, el cenit z y el ecuador QQ’. El diámetro horizontal NS es el horizonte en el que aparece la graduación (en naranja) del acimut, desde 0 en el Norte, pasando por 45 (NE), 90 en el centro (donde se confunden los puntos cardinales E y W con el centro O), 135 (SE) hasta 180 en el Sur. La graduación de la altura se señala (también en naranja) mediante puntos separados de 10 en 10 grados situados inmediatamente al exterior del círculo azul: como estamos viendo la esfera celeste desde un lugar O de latitud φ = 40° la altura de P es de 40° (desde N) y por tanto el punto más alto del ecuador Q tendrá que estar a 50° de altura desde S.
El segmento VV’ es la imagen del paralelo con δ = +23,5°, el que recorre el Sol el día del solsticio de verano. ¿Cuál será la máxima altura del Sol ese día? Pues no tenemos más que mirar la posición del punto V: 73,5° (los 50° de altura de Q más 23,5°).
Pero ahora también podemos precisar numéricamente el acimut del orto: ¿dónde corta el paralelo VV’ al horizonte? En un punto de acimut ligeramente inferior a 60°, unos 59°. Dicho de otra manera, el Sol no sale por el este sino un poco más de 30° desviado hacia el N. Por consiguiente el ocaso tampoco ocurrirá por el W sino unos 31° también hacia el N.
Más todavía: el paralelo VV’ está dividido mediante pequeños puntos en 12 tramos, cada uno correspondiente a una hora de tiempo. Desde V hasta el eje PP’ hay 6 horas y desde el eje hasta V’ otras 6. ¿Cuántos tramos (horas) quedan por encima del horizonte? Contemos: desde V hasta el eje PP’ hay 6 y entre el eje y el orto hay más de una hora, casi hora y media, digamos aproximadamente 1 h 25 m. En total 7 h 25 m. Este es el tiempo que transcurre desde que el Sol sale hasta que llega a su culminación en V el día 22 de junio. Otro tanto pasará por la tarde. El día completo será así de 14 h 50 m.
De manera similar determinaremos con ayuda de la figura 6.9 los datos (máxima altura, acimut de orto y duración del día) en los equinoccios, cuando el sol recorra el ecuador QQ’, o en el solsticio de invierno (paralelo I I’). En el cuadro se resumen todos ellos.
En cuanto al clima que hará en ese lugar solo hay que fijarse en las máximas alturas del Sol, puesto que el factor determinante es la inclinación con que los rayos solares lleguen a la superficie horizontal. En verano está bastante cerca del cenit y hará mucho calor, mientras que los inviernos serán fríos pero no excesivamente. Obviamente consideraciones geográficas (altitud, cercanía al mar sobre todo) matizarán estas primeras conclusiones.
Por último: hay una línea naranja por debajo horizonte y paralela a él. Es la línea del crepúsculo, situada 10° por debajo del horizonte. Cuando el Sol llegue a ella y esté 10° por debajo del horizonte la oscuridad será casi completa y daremos por terminado el crepúsculo. ¿Cuánto tiempo pasa desde que el Sol se pone hasta que llega a esa línea? Mirando los tramos en el paralelo VV’ diremos que en torno a una hora.
| φ = 40º N | Máx. altura | Acimut orto | Duración del día |
| Solsticio Verano | 73,5º | 59º | 14 h 50 m |
| Equinoccios | 50º | 90º | 12 h |
| Solsticio Invierno | 26,5º | 121º | 9 h 10 m |
| Clima templado: veranos cálidos, inviernos no muy fríos | |||
| ¿Pasa el Sol por el cenit en alguna fecha? | NO | ||
| ¿Cuánto dura el crepúsculo el solsticio de verano? | 1 hora | ||
Siempre nos fijamos en las fechas destacadas del ciclo anual. En las fechas intermedias la trayectoria aparente del Sol será la impuesta por su declinación.
Con el planisferio
Naturalmente el Sol no puede aparecer en el planisferio, puesto que no ocupa una posición fija entre las constelaciones, pero sí está dibujada su trayectoria anual aparente, la eclíptica, que es la curva excéntrica de línea verde algo gruesa y trazo discontinuo. Puedes comprobar que esa línea pasa al sur de Aries, cruza los cuernos de Tauro, atraviesa Géminis y Cáncer, roza Régulus (Leo queda al norte), casi toca a Spica de Virgo que se sitúa un poco al S de ella, cruza Libra, deja al sur a Escorpio y Sagitario y atraviesa las últimas constelaciones zodiacales de Capricornio, Aquario y Piscis.

Para determinar dónde veríamos a nuestra estrella en una fecha determinada hay que trazar una recta que una el polo con la marca de esa fecha; la intersección de esa recta con la eclíptica nos dará la posición del Sol ese día. Una manera cómoda de visualizar esa recta es girar la lámina local transparente del planisferio hasta colocarla en esa fecha a las 12 del mediodía; así el meridiano nos servirá como recta que va del polo a la marca correspondiente a ese día.
Por ejemplo, el 30 de diciembre a las 12 horas, el meridiano corta a la eclíptica casi exactamente donde se sitúa una señal con el título M 22 (no es una estrella, sino un objeto destacado si se observa con un telescopio). Pues allí estará el Sol ese día dentro de los límites de la constelación de Sagitario.
Podemos ya averiguar todo lo que queramos. ¿Cuáles serán sus coordenadas? La ascensión recta unas 18h 40m y la declinación δ ≈ 23º S. ¿A qué horas saldrá, cruzará el meridiano y se pondrá? Giremos hasta que M 22 esté saliendo o poniéndose. Obtenemos estos datos:
| Orto | Paso meridiano | Ocaso | |
| Hora | 7:20 | 12:00 | 16:40 |
| Acimut | 120º | 180º | 240º |
| Altura | 0º | 27º | 0º |
Ejercicio 6.1
- El 8 de marzo el Sol se encuentra muy próximo a una débil estrella de magnitud 4. ¿De qué constelación es esta estrella? ¿Cuáles serán las coordenadas ecuatoriales del Sol ese día? Completa una tabla como la anterior para esa fecha.
- ¿Qué día está el astro rey junto a la brillante Régulus?
- ¿Y muy cerca de Spica?
Haz clic aquí para ver la solución