6.6 Trabajos escolares
Las estaciones en el gnomon
Como ya anticipamos en el tema 2, el ciclo de las estaciones puede recogerse fácilmente con el gnomon. Hay que anotar la línea que describe el extremo de la sombra en diversos días a lo largo del año. Lo ideal sería hacerlo una vez al mes, los días 20 o alguno próximo. Cada día se puede marcar de hora en hora, como mínimo.
Lo que es fundamental es que la colocación del gnomon sea la misma todos los días. Como ya dijimos una buena solución es marcar en el terreno (el patio de recreo o donde se vaya a realizar la experiencia) el contorno del tablero para que así pueda quitarse y volverse a poner otro día pero en la misma posición.
La figura siguiente muestra el resultado que se obtendría para un lugar de latitud φ = 40º N. Para otras latitudes próximas habría mínimas diferencias. G es el punto donde se sitúa el estilete, el clavo vertical, cuya sombra estamos analizando.
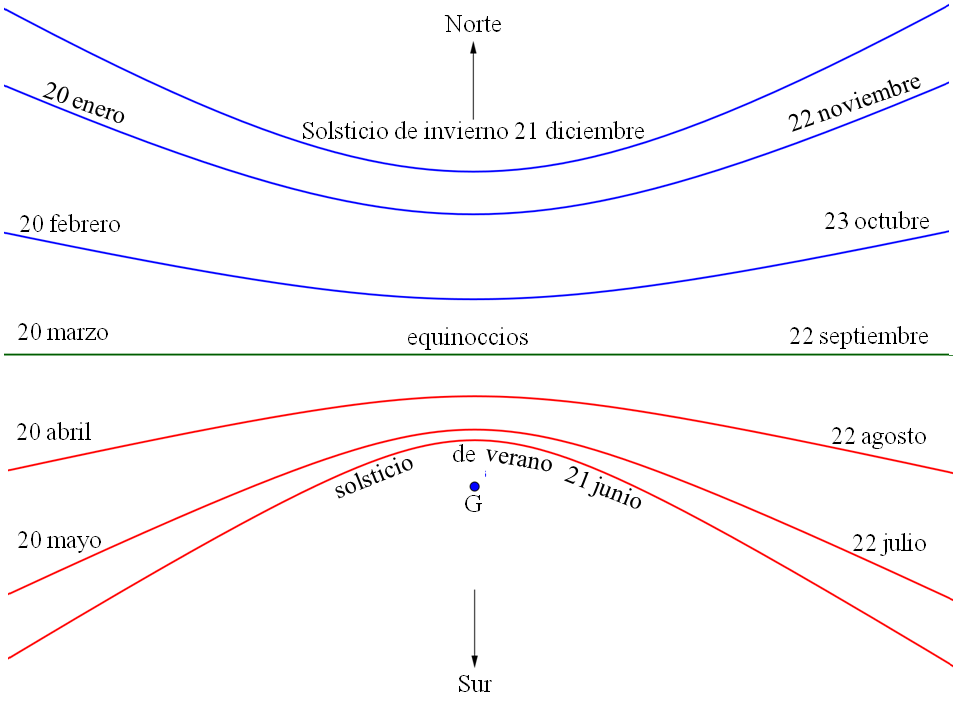
Maqueta con los recorridos diurnos del Sol en solsticios y equinoccios
Sobre un tablero cuadrado (o aún mejor recortado en círculo) que va a representar nuestro horizonte queremos colocar los paralelos que parece describir el Sol (vistos desde un lugar de latitud φ = 40º N) en los días señalados del ciclo de las estaciones: solsticios y equinoccios.
El tablero puede ser una plancha de aglomerado grueso, de 19 mm de espesor, de 45×45 cm. El proceso constructivo podría ser éste:
- Marcamos el centro O (el observador) trazando dos diámetros perpendiculares.
- Dibujamos una circunferencia de centro O y radio R = 20 cm.
- Señalamos los puntos cardinales.
- Dibujamos dos diámetros que formen 30º con el eje Este – Oeste señalando los puntos A, A’, B, B’. Estos serían los puntos de orto y ocaso del Sol en los solsticios.
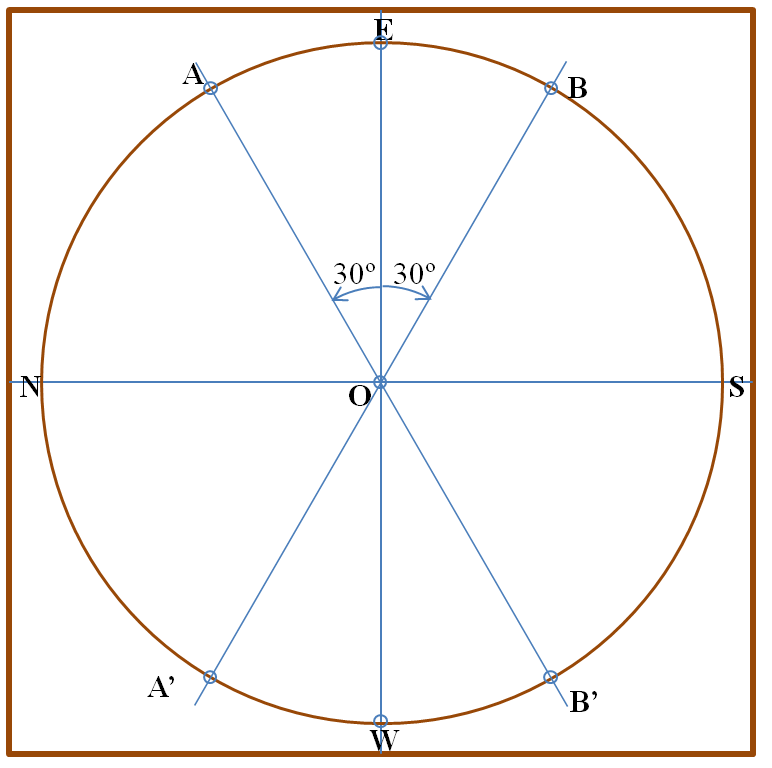
- En los 6 puntos A, E, B, A’, W, B’ tenemos que realizar unos taladros. Estos taladros tienen que formar un ángulo de 50º con el tablero, puesto que esa es la colatitud 90º – φ. Y deben hacerse en la dirección de la circunferencia y con el diámetro del material que vayamos a utilizar para simular los paralelos.
- El material para hacer los paralelos tiene que ser suficientemente flexible, para poder darles forma circular, y rígido para que se sustenten sin dificultad. Se puede utilizar alambre de unos 2 mm de diámetro o varillas de plástico también muy finas.
- La varilla equinoccial debe ser una semicircunferencia de radio R = 20 cm más 2 cm por cada lado para insertar en los taladros. Resulta una longitud = π·R + 4 = 69 cm. Y debe sujetarse en los taladros de los puntos E y W.
- La varilla del solsticio de verano debe medir 2·π·R·cos 23,5º·15/24 + 4 = 76 cm y se insertará en los taladros A, A’.
- La varilla del solsticio de invierno tendrá una longitud = 2·π·R·cos 23,5º·9/24 + 4 = 47 cm y se insertará en los taladros B, B’.
- Será muy conveniente colocar otra varilla (el meridiano) con la misma longitud que la ecuatorial (la de los equinoccios) y alojada en nuevos taladros (estos verticales) hechos en los puntos cardinales N y S. Puede servir de apoyo para que las otras se sujeten convenientemente. La ecuatorial debe alcanzar el meridiano a 50º de altura, la del solsticio de verano a 73,5º y la del solsticio de invierno a 26,5º.
Esfera armilar
Como ya vimos en los Trabajos escolares de la lección 4, en el globo celeste están señaladas las posiciones del Sol entre las constelaciones cada 10 días mediante puntos rojos. Estos en conjunto forman la eclíptica. Así podremos reproducir los recorridos aparentes del Sol en cualquier fecha y en cualquier latitud observando sus puntos de salida y puesta, su máxima altura meridiana y el número de horas que permanece por encima del horizonte, es decir, la duración del día. La esfera armilar es el mejor modelo para entender el ciclo de las estaciones desde un punto de vista geocéntrico.
Vamos a corroborar con la esfera armilar los resultados obtenidos en los ejercicios de este tema.
Coloca la esfera para una latitud φ = 40º N. Como ya sabes el Polo Norte celeste debe quedar a 40º de altura por encima del punto cardinal N. Busca, en la eclíptica, los puntos rojos que señalan solsticios y equinoccios. Haz girar la esfera para observar el acimut y la hora de salida, la máxima altura meridiana, el acimut y la hora de puesta. Puedes así calcular cuántas horas de luz habrá en cada una de esas fechas. Contrasta tus resultados con la tabla de la página 9.
Puedes repetirlo para las diferentes latitudes que se han usado en esta lección (10º N, 72º N y 35º S) verificando los resultados (ejercicios 6.2, 6.3 y 6.4). También puedes simular estos recorridos en las latitudes extremas (en el ecuador y en ambos polos).
Modelo clásico con un globo terráqueo y un foco central
Si utilizamos un foco de luz central que haga las veces del Sol y un globo terráqueo corriente podemos reproducir con toda fidelidad lo que sucede a medida que la Tierra órbita alrededor de nuestra estrella. Aquí ya el modelo es heliocéntrico.
Los globos terráqueos suelen tener ya el eje inclinado los pertinentes 23,5º con respecto a la peana que sirve de soporte. Desplazando el globo alrededor del foco central procurando que el eje quede siempre con la misma orientación podremos observar lo que ocurre en los puntos más importantes (solsticios y equinoccios). El desplazamiento del globo debe hacerse manteniendo éste a la misma altura del foco, con lo que recorrerá el plano de la eclíptica.
Por ejemplo, cuando el eje esté inclinado hacia el foco (con el polo Norte más cerca del foco y el Sur más alejado) estaremos visualizando la situación en el solsticio de verano (22 de junio). Manteniendo en su posición el globo y haciéndolo girar (para reproducir el movimiento de rotación de la Tierra) podremos observar que el polo Norte queda siempre iluminado por la luz del foco mientras el Sur está sumido en la oscuridad. También se puede contemplar en qué punto del globo cae la luz del foco en perpendicular, así como estimar cuántas horas de luz habrá en cualquier punto de la Tierra.
La imagen corresponde aproximadamente a la situación opuesta (22 de diciembre, solsticio de invierno). Al polo Norte no llega la luz del foco (por mucho que rote el globo) y, en cambio, el polo Sur estará iluminado las 24 horas del día.
El terminador de la Tierra
En la práctica anterior nos apareció siempre una dificultad: que la línea de luz-sombra en el globo no aparecía claramente definida, haciendo muy difícil cuantificar el número de horas de luz diaria en un punto cualquiera de la Tierra.
La maqueta que se presenta ahora propone simple- mente visualizar el terminador de la Tierra mediante un plano vertical que “abrace” al globo. Ese plano debe ser perpendicular al radio Sol-Tierra y debe pasar por el centro de ésta, de modo que todo el hemisferio que esté “mirando” hacia el Sol es el que está iluminado, mientras que en el otro (en todos los puntos que estén “detrás”) es de noche.
En las fotografías adjuntas puede verse el globo terráqueo, con su eje de rotación inclinado 23,5º, y un plano que es siempre vertical pero que puede rotar adoptando diferentes posiciones, tal y como ocurre con el plano del terminador de la Tierra.
Incorporando este plano que representa el termi- nador de la Tierra los alumnos pueden acercarse al globo terráqueo y observar directamente en él todos los fenómenos propios del ciclo anual con mayor claridad. Además es fácil cuantificar alguno de ellos, especialmente la duración del día en cualquier lugar de la Tierra y en cualquier fecha (sobre todo en solsticios y equinoccios) gracias a la red de meridianos terrestres, sin más que contar el número de meridianos que quedan en la zona iluminada para una latitud determinada. La “demostración” visual de la igual duración de días y noches en los equinoccios en cualquier lugar de la Tierra gana mucho con la incorporación del plano del terminador.
En la figura de la derecha se pueden apreciar varias pegatinas colocadas en un mismo meridiano pero a diferente latitud. El punto azul corresponde a 40º N, el rojo está en el círculo polar ártico y el amarillo a 80º N. La posición del plano del terminador en esta figura corresponde al 22 de junio, solsticio de verano en el hemisferio norte. El polo Norte está “delante”, es decir, en la zona iluminada. Haciendo rotar el globo se verá cómo el punto amarillo está siempre claramente dentro de la zona iluminada, que el punto rojo está en el límite de esa
zona en la que hay Sol las 24 horas, mientras que el punto azul sí que pasa una parte de su trayectoria por “detrás”. Recorriendo el paralelo 40º N y contando el número de meridianos (trazados de 15º en 15º, cada uno correspondiente a una hora de rotación) podemos averiguar cuántas horas pasará el punto azul en la cara “iluminada” y cuántas en la cara “oscura”, lo que equivale a determinar cuál es la duración del día y de la noche en esa latitud y en esa señalada fecha del solsticio de verano.
En la fotografía (izquierda) se aprecia también una pegatina verde colocada en un lugar a unos 40º de latitud pero ahora Sur. Las flechas blancas indican la dirección de los rayos del Sol, correspondientes, como antes al 22 de junio. Haciendo rotar el globo puede reproducirse la situación típicamente invernal de ese punto del hemisferio sur, con días muy cortos y noches largas.
La figura (derecha) muestra la situación inversa. Las flechas blancas siguen indicando la procedencia de la luz solar. Ahora es el polo Sur el permanentemente iluminado, mientras que el casquete polar Norte,
por mucho que rote el globo terráqueo, siempre permanecerá en la cara “oscura”. Con los adhesivos a diferentes latitudes pueden cuantificarse la duración de días y noches en cualquier lugar de la Tierra en el solsticio de invierno (22 de diciembre).
También se puede apreciar con bastante nitidez la inclinación de la luz solar con respecto al plano del horizonte en cualquier lugar de la Tierra y en la fecha que se desee, así como proceder a averiguar en qué puntos de nuestro planeta verán al Sol en el cenit.
La última fotografía muestra una posición equinoccial, con el eje de rotación del globo inmerso en el plano del terminador. En esta posición es claro que todos los paralelos, independientemente de la latitud, estarán divididos en dos partes iguales por el plano del terminador, es decir, tendrán una mitad en día y la otra en noche: lo que muestra que esas fechas (21 de marzo y 23 de septiembre) en cualquier lugar de la Tierra el día y la noche durarán 12 horas.
La construcción práctica de este plano conlleva algunas pequeñas dificultades, puesto que debe poder girar (para adecuarse a la posición relativa Sol-Tierra) y debe permitir el paso del eje de rotación. Presentamos aquí una posible solución, pero es evidente que el ingenio de cada maquetista resolverá esos pequeños problemas de una forma u otra.
Todas las fotografías de estos Trabajos escolares son del Aula de Astronomía de Fuenlabrada.
La Tierra paralela
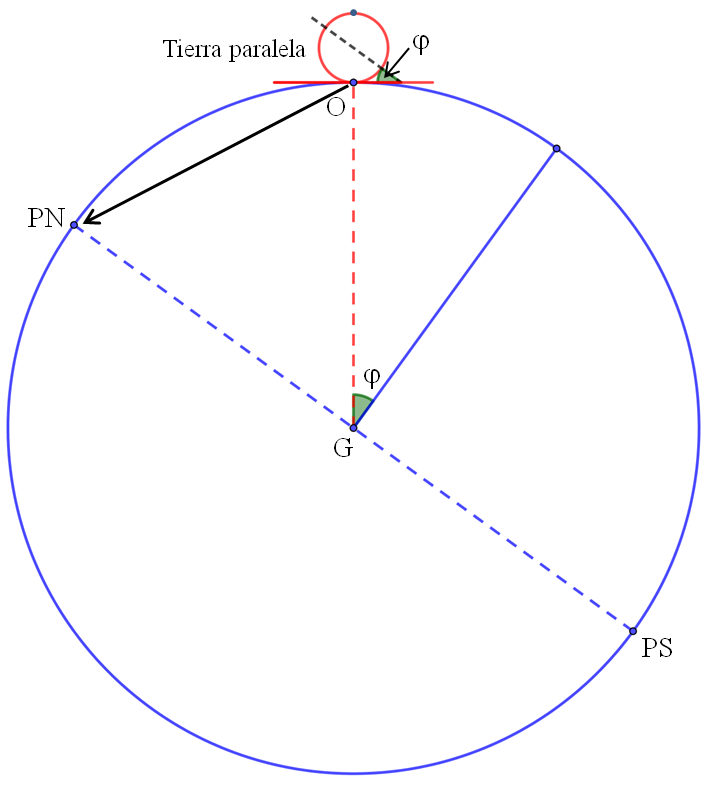
Es un globo terráqueo colocado en paralelo a la esfera terrestre. Para conseguir esa disposición tenemos que hacer que el eje del globo quede paralelo al terrestre, apuntando lo más exactamente posible al Polo Norte celeste. Esto se logra haciendo que el eje del globo forme con el suelo un ángulo igual a nuestra latitud (φ) y orientándolo en la dirección Norte – Sur como se muestra en la fotografía. El lugar en el que estamos tiene que quedar en el punto más alto del globo.
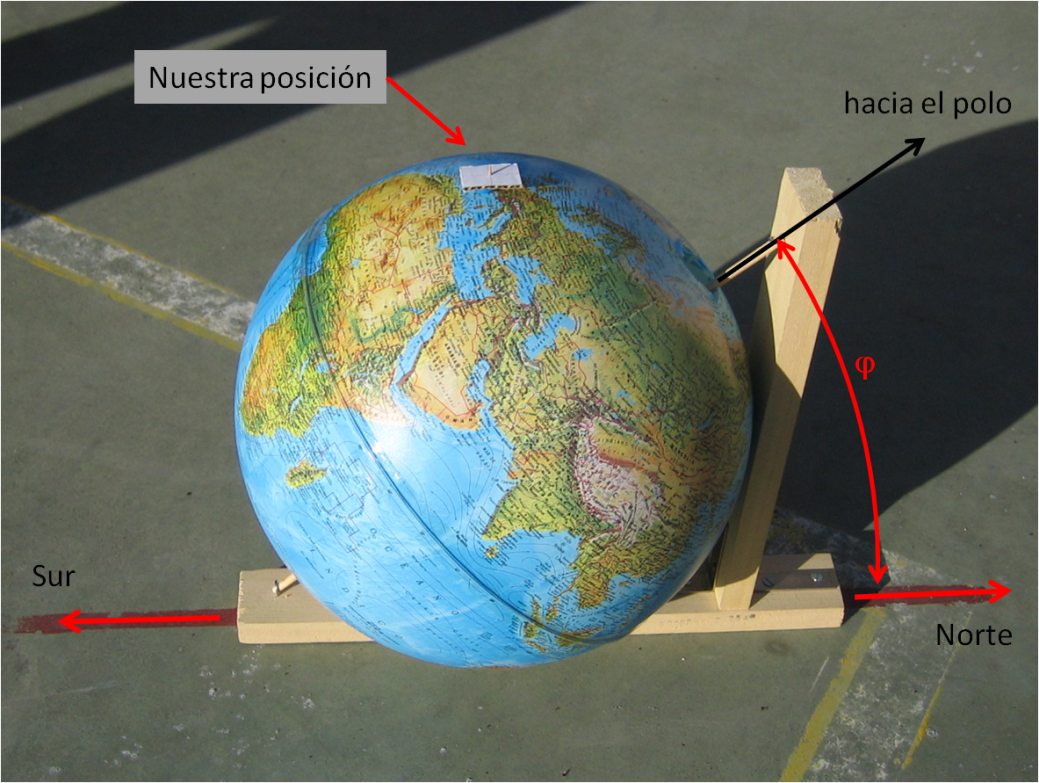
¿Qué partido podemos sacarle a esta mini-tierra orientada?
- La esfericidad de la Tierra es algo que todos “sabemos” pero que no siempre tenemos verdaderamente interiorizado. Si pedimos a alguien que nos señale en línea recta hacia el centro de la Tierra, o hacia Nueva Zelanda, todos extenderán el brazo apuntando hacia abajo. Sin embargo si preguntamos por el Polo Norte geográfico es muy probable que se apunte en horizontal y hacia el Norte. Pero esa recta horizontal será tangente a la esfera terrestre y se irá separando de ella. Nuestro horizonte (el de cualquier punto O) siempre deja al cielo por encima y a la Tierra por debajo.
En el globo se ha colocado un pequeño rectángulo pegado con un poco de plastilina y con un pequeño trozo de madera fina en vertical (un fragmento de palillo). Con este modelo resulta evidente que cualquier observador O, en cualquier punto de la Tierra, siempre verá su horizonte plano y toda la Tierra por debajo de él. Así, si quisiéramos indicar una línea recta que fuera desde O hasta el Polo Norte geográfico, esa recta tiene que dirigirse, por supuesto hacia el N, pero también deberá apuntar por debajo del horizonte.
- Otra cuestión que salta a la vista es que el globo está iluminado por la luz solar exactamente igual que nuestro planeta. Por tanto donde la tierra paralela esté iluminada será de día (en la fotografía toda África y buena parte de Asia y de Europa) y donde no, de noche (el polo Norte, extremo oriental de Asia y prácticamente toda Siberia, ver la primera fotografía). Como el Sol avanza de Este a Oeste tampoco es difícil ver dónde se está poniendo en ese momento (Siberia, Mongolia, China, Filipinas) o saliendo (Brasil).
- Colocando diferentes “horizontes” en varios puntos de un mismo meridiano se puede observar cómo la longitud de la sombra del “mini gnomon” varía lo que nos indica la altura del Sol en cada uno de esos lugares.
- Se puede buscar cuál es el único punto de la superficie terrestre en el que el Sol está cayendo a plomo en ese momento, moviendo el horizonte portátil hasta conseguir que el pequeño gnomon no proyecte ninguna sombra, señal de que ese punto (cerca de Madagascar) tiene al Sol en su cenit.
- Si la sombra se dirige exactamente hacia el Norte, es que el Sol (en ese punto) se ve en dirección Sur, es decir que allí es mediodía. Es fácil comprobar que eso ocurre en todos los lugares de un mismo meridiano.
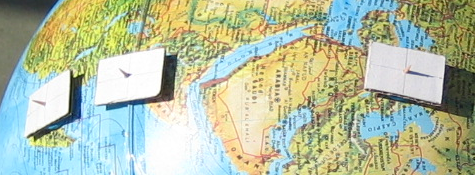
- Por último es posible hacer algún pequeño truco de magia. ¿Podríamos averiguar mediante la tierra paralela si en este momento la sombra de la torre Eiffel cruza el Sena o no? Si construimos un horizonte portátil con un plano de París y en él, a la misma escala, ponemos una figura de dicha torre y lo colocamos todo debidamente orientado sobre París en el globo podremos ver directamente lo larga que es su sombra.
Todas las fotografías de la “Tierra paralela” son del Instituto Rey Pastor, salvo esta última que es de Esteban Esteban (Aula de Astronomía de Durango).