7.9 Ecuación de tiempo
La idea simple de “día” como una rotación de la Tierra sobre sí misma en 24 horas, como tantas otras nociones intuitivas en Astronomía, debe ser precisada. Nuestra vida está regida por el día solar que puede definirse como el tiempo entre dos mediodías consecutivos. Si comenzamos con el Sol en el meridiano del punto A (y el centro de la Tierra en T), el siguiente mediodía se dará en la posición T’A’, pero para llegar allí la Tierra ha tenido que rotar 360º + α y ese ángulo adicional debe coincidir con el arco recorrido por la Tierra desde T hasta T’. Así que para efectuar una rotación (360º) necesita algo menos de 24 horas, exactamente 23 h 56 m, periodo llamado día sidéreo: si al comienzo (T) cierta estrella está en el meridiano de A, después de una rotación esa misma estrella volverá a estar en el meridiano de A como indica el paralelismo de ambos vectores.
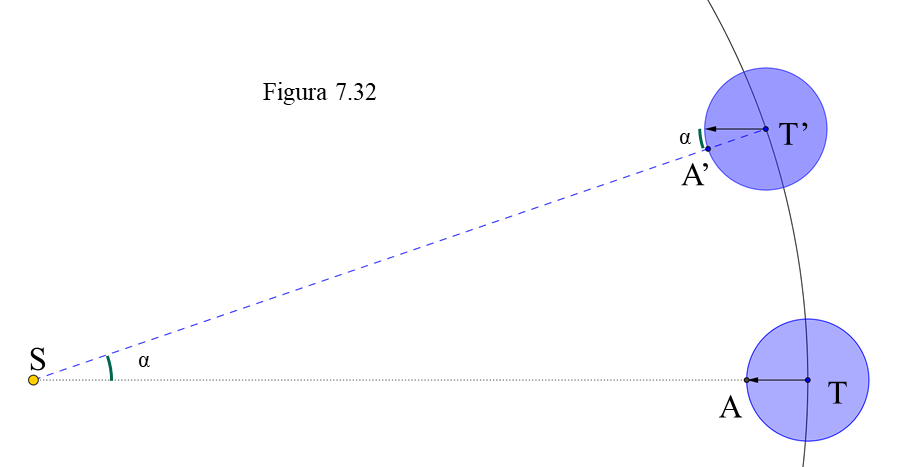
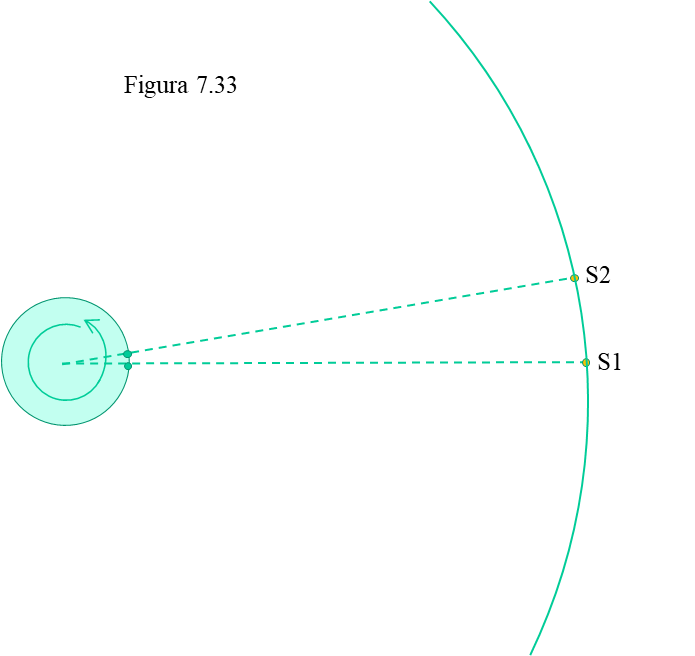
En la figura 7.33 se ha situado la Tierra en el centro (inmóvil, pero rotando) y el Sol avanzando por la eclíptica. Desde el punto de vista de las apariencias es totalmente equivalente a la anterior. Así pues la unidad básica de tiempo es el día solar, tal y como se ha definido y que se divide en 24 horas.
Como siempre uno piensa, ingenuamente, que después de 24 horas volveremos a tener al Sol culminando en el meridiano. Pues no.
Supongamos que estamos situados en un lugar del meridiano de Greenwich, para ahorrarnos la corrección por longitud. Allí se supone que el mediodía tiene que ocurrir a las 12 en punto (a las 13:00 hora oficial en otoño e invierno o a las 14:00 entre abril y octubre). Si anotamos la posición del Sol siempre a esa hora, para nuestra sorpresa, obtenemos esta bonita figura:
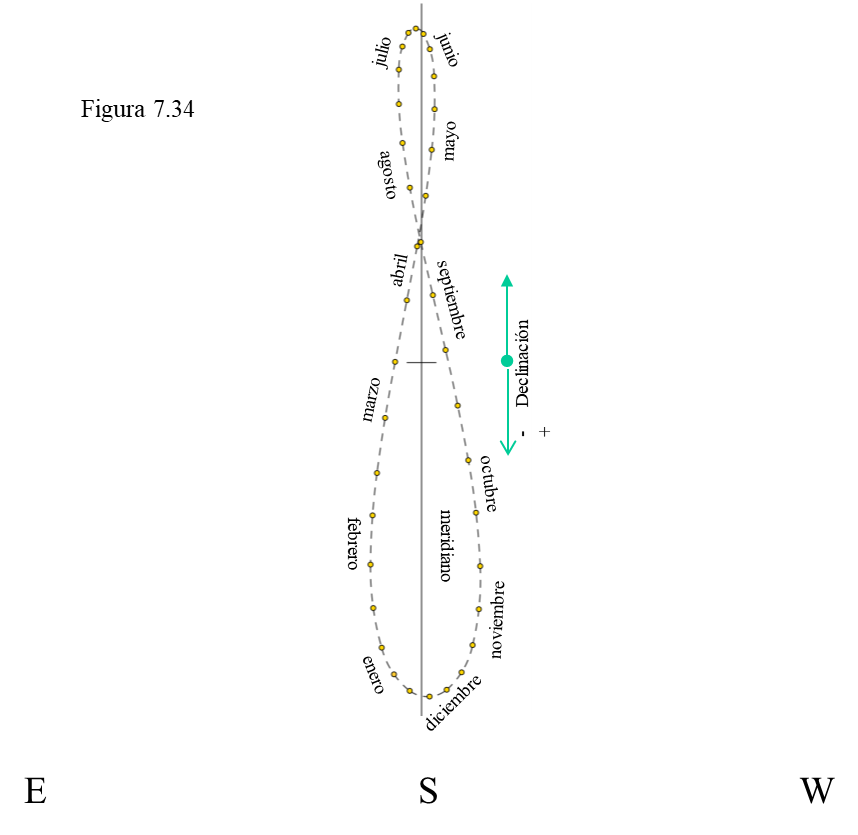
Obviamente el Sol sube y baja cambiando de declinación y de máxima altura meridiana a lo largo del año, pero también se adelanta o se retrasa algo. Por ejemplo, en noviembre, a las 13:00 (horario de invierno) el Sol está a la derecha (al oeste) del meridiano, es decir, ya lo ha cruzado por lo que un reloj de Sol estará señalando más de las 12 en punto. En cambio, en febrero, a las 13:00 de nuestro reloj de pulsera, el Sol está a la izquierda (Este) del meridiano, aún no ha llegado a él y un reloj de Sol marcaría menos de las 12.
Esta curva en forma de 8 estilizado recibe el nombre de “analema”. ¿A qué se debe? Pues básicamente a dos cuestiones: (a) el irregular avance de la Tierra a lo largo de su órbita elíptica ligeramente excéntrica tal y como establece la 2ª ley de Kepler, que veremos con más detalle en el capítulo 9, que equivale al avance aparente del Sol por la eclíptica y (b) la inclinación de la eclíptica sobre el ecuador por lo que la traslación y la rotación no se efectúan en un mismo plano. Ambos factores hacen que el Sol a veces esté adelantado y otras atrasado (tal y como se aprecia en el “analema”) con respecto a su posición media y por tanto la hora solar verdadera (la que da un reloj de Sol) y la hora solar media no coincidan. La diferencia entre ambas se conoce como “ecuación de tiempo” y la siguiente gráfica nos da sus valores (hora media – hora solar verdadera) a lo largo del año:
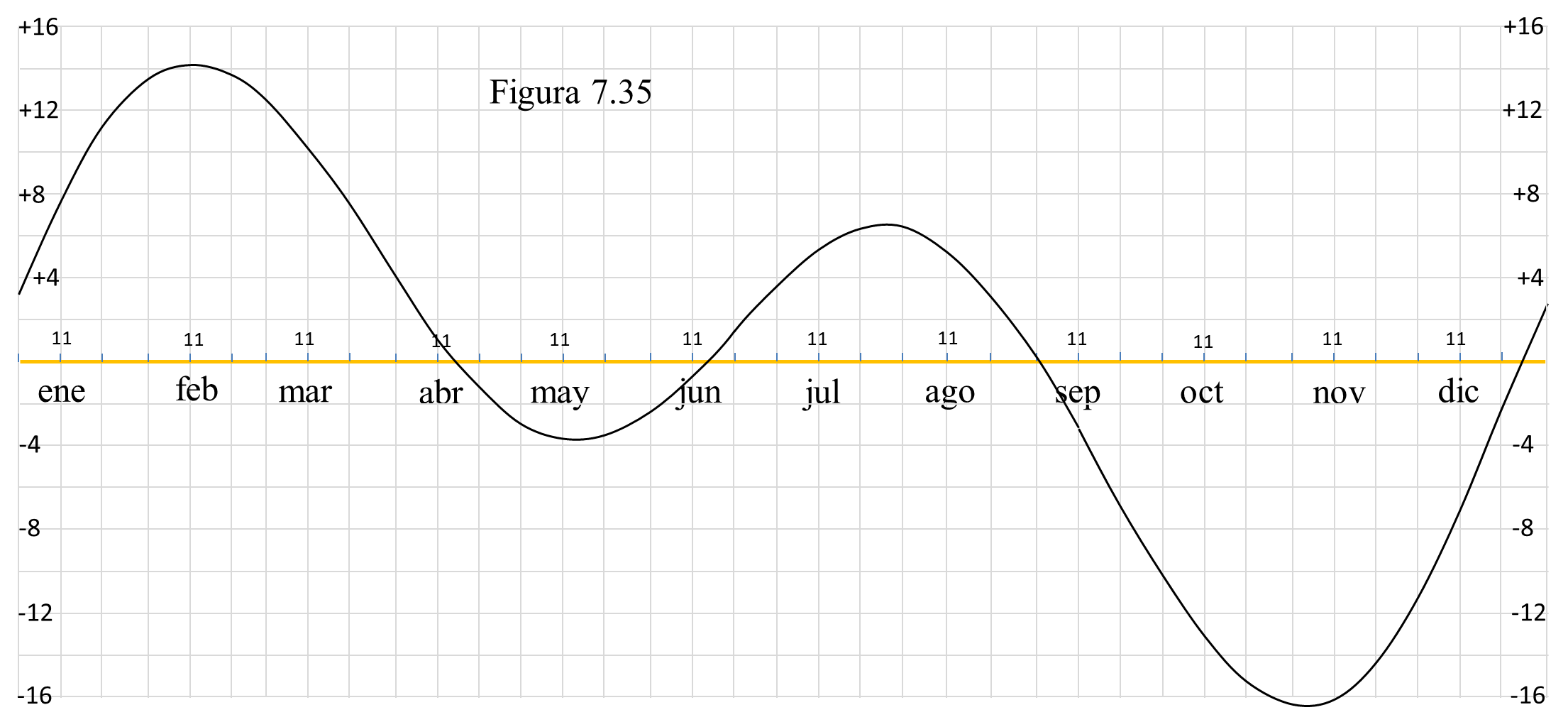
En el eje horizontal se sitúan los meses del año con tres marcas correspondientes a los días 1, 11 y 21 aunque solo el día 11 está numerado. En el vertical se sitúa la corrección (en minutos) que hay que hacer a la hora que marca el reloj de Sol para pasar a la hora media. El día 11 de marzo, por ejemplo, el gráfico indica una corrección de +10. Eso quiere decir que a la hora que marque el reloj de Sol tendremos que sumarle 10 minutos para pasar a la hora media (aparte de las correcciones por longitud y por ahorro de energía). En cambio, el 11 de octubre leemos en el gráfico que el valor de la ecuación de tiempo es de -13 minutos, por lo que a la hora solar verdadera tendremos que restarle esos 13 minutos para tener la hora solar media.
Pulsa aquí si quieres ver una explicación más detallada.
En resumen, para conocer la hora oficial a partir de la que marca el reloj de Sol es preciso hacer las siguientes correcciones:
- Longitud geográfica: añadir (para un lugar al Oeste) o restar (para un lugar al Este) la diferencia de longitud convertida en tiempo (15o = 1 hora).
- Añadir una hora desde noviembre hasta marzo y dos entre abril y octubre.
- Ecuación de tiempo: añadir o restar los minutos que marca el gráfico anterior según la época del año.
HORA OFICIAL = HORA SOLAR VERDADERA + CORRECCIÓN POR LONGITUD + CORRECCIÓN GUBERNAMENTAL + ECUACIÓN DE TIEMPO
Por ejemplo, ¿cuál será la hora oficial el 1 de julio en Castellón cuando allí un reloj de Sol señale las 12 en punto? No hay que hacer ninguna corrección por longitud, pero como estamos en pleno verano los relojes de pulsera van dos horas adelantados, así que serían las 2 pm. Pero hay que tener en cuenta la ecuación de tiempo cuyo valor para el 1 de julio es de +4 minutos que habrá que sumar: la hora oficial será 14h 04mn
Al revés, ¿qué marcará un reloj de Sol en Castellón el 10 de marzo a la 1 pm hora oficial? Como seguimos en el meridiano de Greenwich nos volvemos a ahorrar la corrección por longitud. El 10 de marzo aún estamos en horario de invierno y el reloj de Sol debería marcar una hora menos, es decir, las 12 en punto. Debería ser mediodía. Pero no, la dichosa ecuación de tiempo el 10 de marzo es de +10 minutos (el reloj de pulsera marca 10 minutos más que el de Sol) por lo que la hora solar verdadera resulta ser las 11h 50mn. Aún no es mediodía; el Sol ese día va “retrasado” con respecto a su posición media y se verá algo a la izquierda (hacia el Este) del meridiano.
Ejercicio 7.5
- ¿Cuál será la hora oficial en Sevilla (longitud 6º Oeste) el 15 de agosto cuando el reloj de Sol señale las 3 de la tarde?
- ¿Cuál será la hora oficial en Bilbao (longitud 3º Oeste) el 5 de febrero cuando el reloj de Sol señale las 10 de la mañana?
Haz clic aquí para ver la solución