9.2 La revolución copernicana
Otro de los grandes hitos de la Ciencia es el De Revolutionibus Orbium Coelestium (Sobre las revoluciones de las esferas celestes) publicado por Nicolás Copérnico en 1543, poco antes de morir. Allí cambiaba brutalmente los dogmas hasta entonces imperantes y sostenía que la Tierra es sólo uno más entre los planetas que rodean al Sol y que circula, como todos, en una órbita que es casi una circunferencia. Con este enorme cambio de paradigma Copérnico resolvía de una vez por todas muchas de las deficiencias teóricas y lograba un modelo unificado. Vamos a ir viendo cómo el sistema heliocéntrico consigue explicar de una forma absolutamente coherente todos los detalles observados.
La elongación
Ya hemos hablado de ella en el tema 5, La Luna: la elongación es la distancia angular entre el Sol y un planeta, siempre vistos ambos desde la Tierra, claro, que es donde estamos y desde donde hacemos nuestras observaciones, es decir el ángulo STP. Y puede ser Este (si el planeta se ve a la izquierda del Sol) u Oeste (si se ve hacia la derecha, como en la figura 9.8).
Si la elongación es 0º es que el planeta y el Sol están en la misma línea visual y se dice que el planeta está en conjunción (con el Sol y, desde luego, sería invisible) y si es 180º es que se encuentra justo al otro lado, o en oposición (al Sol claro), y entonces sí que se verá estupendamente por la noche. Cuando la elongación de un planeta es de 90º se dice que está en cuadratura. Todos son nombres bastante razonables.
Ya se sabía que, con respecto a la elongación, hay dos grupos de planetas: Marte, Júpiter y Saturno podían tener cualquier elongación, pero Mercurio y Venus siempre se ven bastante cerca del Sol; la de Mercurio nunca sobrepasa los 27º y la máxima de Venus es de unos 47º.
Esto tiene todo su sentido dentro del sistema heliocéntrico y permite ordenar claramente los planetas: Mercurio y Venus tienen que tener órbitas interiores a la terrestre, mientras que los demás deben estar más lejos.
Como se ve en la figura 9.9, la elongación de Venus tiene un tope máximo en V2 y en V4, precisamente cuando la visual TV sea tangente a la órbita circular de Venus. Otras posiciones destacadas de Venus son V1 (conjunción inferior) y V3 (conjunción superior). Y una elongación mayor, sería imposible, pues Venus no puede estar nunca en una posición como la V5.
Al mismo tiempo y debido a que es un planeta interior Venus, y Mercurio, tienen fases como la Luna. Fueron observadas por primera vez por Galileo entre octubre de 1610 y febrero de 1611. Este hecho le sirvió para reforzar el modelo heliocéntrico del Sistema Solar.
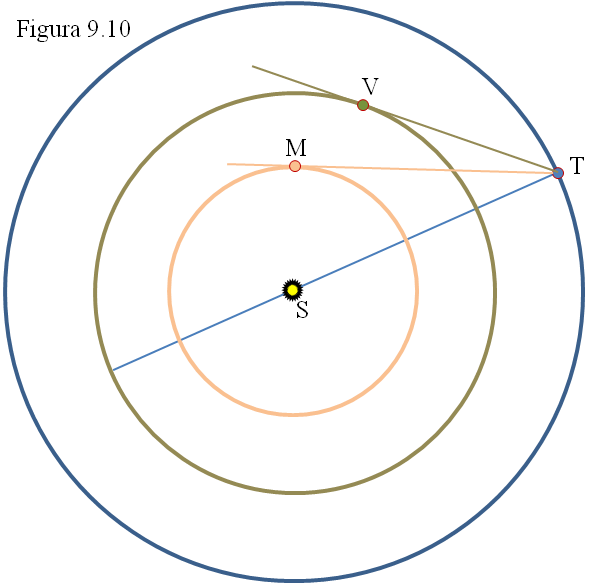
Otro tanto ocurre con Mercurio, pero dado que su máxima elongación es solo de 27º, se deduce que su órbita debe ser aún más “pequeña” que la de Venus, figura 9.10.
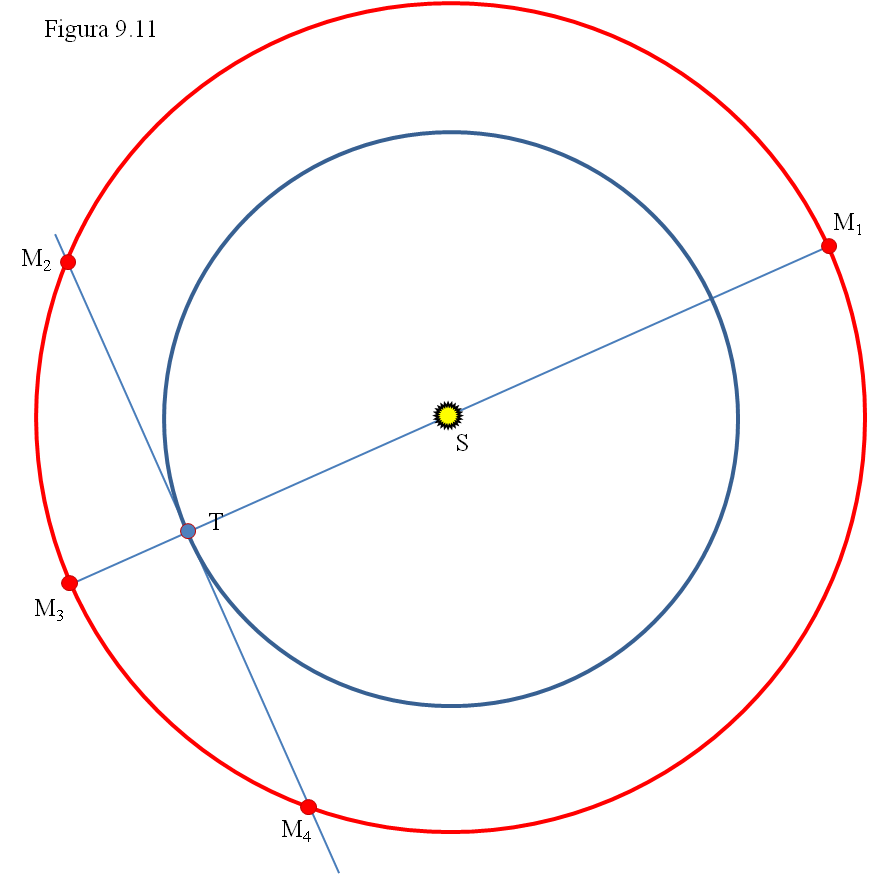
En cambio para Marte (Júpiter o Saturno), la situación es diferente, el hecho de que su elongación pueda tomar cualquier valor implica que su órbita tiene que ser exterior a la terrestre. Algunas posiciones destacadas serían: M1 (conjunción), M2 (cuadratura Este), M3 (oposición) y M4 (cuadratura Oeste), figura 9.11.
Así pues el orden de los planetas quedaba ya enteramente ajustado: Mercurio, Venus, la Tierra, Marte, Júpiter y Saturno. Los tres exteriores se ordenan en función del tiempo que tardan en recorrer el Zodiaco; siguiendo la misma pauta cabe suponer que Mercurio sea el más rápido y Venus el siguiente en velocidad orbital. ¿Por qué entonces los dos planetas interiores tardan de media un año en recorrer el Zodiaco vistos desde la Tierra? Dentro de un momento lo veremos.
Retrogradaciones
¿Da cuenta el sistema heliocéntrico de los bucles aparentes de los planetas? Naturalmente que sí. Veamos cómo. En la figura 9.12 aparecen las órbitas de la Tierra (en azul) y de Marte (en rojo) con el Sol en el centro. En ambas están marcadas las sucesivas posiciones de los dos planetas en las mismas fechas (de 30 en 30 días). Fíjate que Marte avanza bastante más despacio por su órbita que la Tierra.
Para simular dónde vemos a Marte desde la Tierra se han unido las posiciones simultáneas prolongando la visual hacia la derecha, hasta el fondo estrellado donde aparecen las constelaciones zodiacales (que, en realidad, tendría que estar mucho más alejado). Así, en las posiciones 1, nosotros veríamos a Marte donde se sitúa el número 1 de la derecha, al principio de Libra. Como la Tierra circula más deprisa, adelanta a Marte justo en las posiciones 5 de ambos, que corresponden a la oposición y que es también el momento en que ambos planetas están más cerca entre sí (el instante, por tanto, en el que lo veremos más brillante).
Observa el recorrido aparente de Marte siguiendo los puntos de la derecha en su orden; entre el nº 1 y el 4 avanza en su sentido habitual, atraviesa Libra y llega al final de Escorpio, pero de 4 a 5 y de 5 a 6 vuelve para atrás hasta el principio de Escorpio, retrograda, y el centro de la marcha atrás es exactamente el punto 5; a partir de las posiciones 6 el planeta rojo, visto desde nuestro observatorio móvil que es la Tierra, retoma su sentido de avance normal, vuelve a atravesar Escorpio y sigue por Sagitario. Esto es ni más ni menos que el recorrido aparente de Marte a través del Zodiaco.
En esta otra animación que representa una retrogradación de Marte, se reproduce mucho mejor.
A la izquierda están las órbitas de la Tierra y Marte recorridas a sus velocidades reales y la línea TM que une ambos planetas; en la parte derecha se sitúa la Tierra en el centro del Zodiaco y se dibuja el vector T’M’ paralelo a la recta TM de la izquierda; así se puede comprobar qué es lo que le vemos hacer aparentemente al planeta rojo: efectivamente va recorriendo las constelaciones en su sentido habitual, pero de vez en cuando (cuando nuestro planeta le adelanta por dentro) Marte parece detenerse, durante un breve tiempo retrograda para volverse a frenar y recuperar su marcha normal en el sentido de los signos.
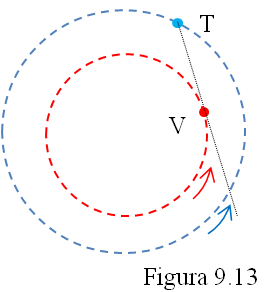
También con los planetas interiores ocurre lo mismo, solo que ahora la retrogradación aparente tal y como la vemos desde la Tierra (figura 9.13) se produce cuando nuestro planeta es adelantado por el interior. El centro del bucle coincide con la conjunción inferior.
Periodos orbitales
Vamos a seguir los procedimientos históricos para determinar otro dato importante de los planetas: su período de traslación (T) alrededor del Sol. Desde la Tierra no podemos medir directamente el tiempo que tarda Venus en dar una vuelta alrededor del Sol, pero sí podemos contar el tiempo que transcurre desde una conjunción inferior a la siguiente (desde el centro de una retrogradación hasta el centro de la siguiente, es decir, su período sinódico): como ya vimos resulta ser de 584 días. Esta cuenta no puede hacerse con las conjunciones, que son inobservables, pero sí con las máximas elongaciones. Ahora sólo queda hacer números.
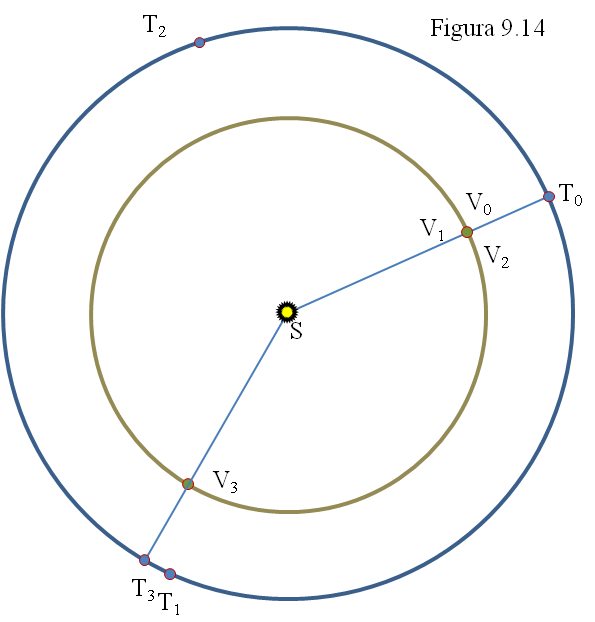
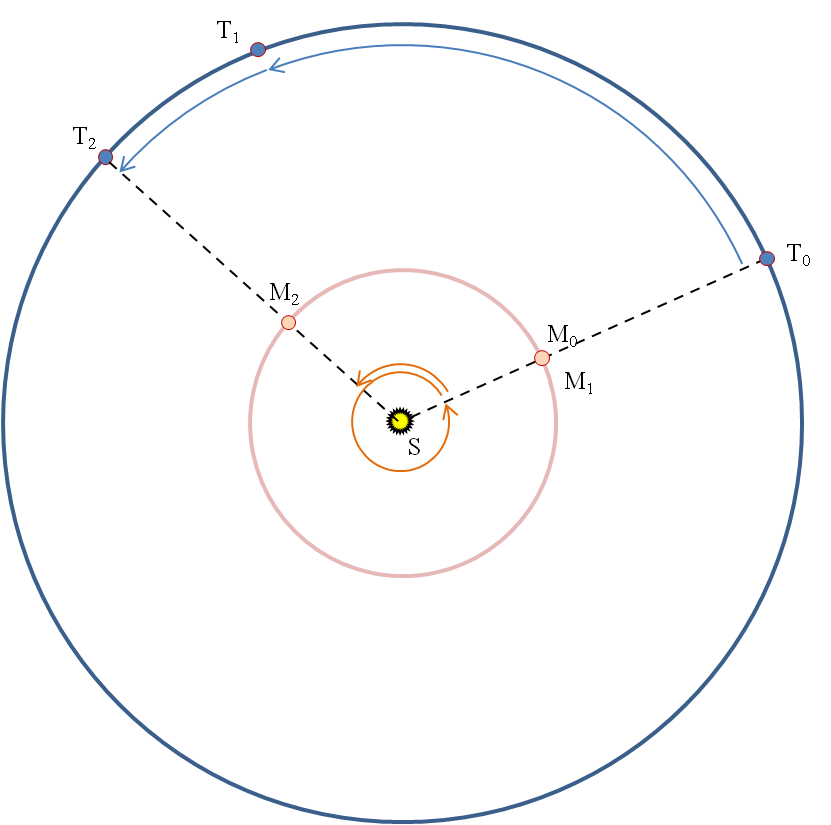
Las posiciones de Venus y de la Tierra (figura 9.14), desde una conjunción inferior en V0T0 hasta la siguiente conjunción inferior en V3T3, tienen que ser las indicadas en la figura 4. Como Venus va más deprisa que la Tierra, en el tiempo que tarda en completar una vuelta (de V0 a V1) nuestro planeta ha avanzado menos de 360º y se coloca en T1; en otro circuito completo de Venus (de V1 a V2) la Tierra se situará en T2 y finalmente volverán a coincidir en V3 T3. Mientras Venus ha dado dos vueltas y media largas, la Tierra sólo ha dado algo más de una y media.
Teniendo en cuenta que la Tierra da una vuelta (360º) en 365,25 días, ¿qué ángulo ha avanzado la Tierra en esos 584 días que van de T0 a T3?
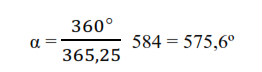
¿Qué ángulo ha recorrido Venus en ese mismo tiempo? Ten en cuenta que Venus ha dado una vuelta más que la Tierra.
575,6º + 360º = 935,6º
¿Cuántos días tarda Venus en avanzar 360º? Es decir, ¿cuál es su periodo orbital?
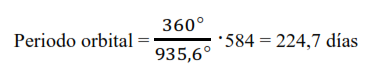
Ejercicio 9.3
Repite los cálculos para Mercurio, sabiendo que circula aún más aprisa que Venus y que su período sinódico es de 116 días. En ese poco tiempo a Mercurio le da tiempo de completar una vuelta y alcanzar de nuevo a la Tierra.
Haz clic aquí para ver la solución
¿Por qué, entonces, el período sidéreo de Mercurio y de Venus es de un año? Se entenderá mejor con el primero. Visto desde la Tierra, Mercurio siempre se ve cerca del Sol (recuerda que su máxima elongación es de solo 27º). Supongamos que un día el Sol, visto desde la Tierra, está en el centro de la constelación de Virgo; Mercurio podrá estar un poco “por delante” (a la izquierda, hacia el Este) quizá ya en Libra y otras veces se le verá algo “atrasado” todavía en Leo, pero, por término medio, lo veremos recorrer el cinturón zodiacal a la misma velocidad que el Sol, por lo que su periodo sidéreo tiene que ser un año.
Otro tanto ocurre con Venus con la diferencia de que, al ser la órbita de éste último comparativamente mucho mayor, puede adelantarse o atrasarse bastante más que Mercurio, pero en todo caso y siempre como media Venus recorrerá el Zodiaco, visto desde la Tierra, en el mismo tiempo que el Sol, un año.
Para los planetas exteriores la situación es similar, sólo que ahora es la Tierra la que tiene una órbita pequeña y por eso, de nuevo por término medio, es como si nuestro planeta estuviera en la posición del Sol y entonces el periodo sidéreo de Júpiter, por ejemplo, tiene que coincidir con su periodo orbital. Lo que nos queda por hacer es comprobar que el periodo sinódico observado coincide con el deducido numéricamente.
Veámoslo para Júpiter. Estos son los datos:
Sd = periodo sidéreo = T = periodo orbital = 11,86215 años = 4.332,65 días
Sn = período sinódico = 398,9 días Período orbital de la Tierra = 365,25 días
Comprobemos. He aquí (figura 9.15) las posiciones de ambos planetas entre dos oposiciones consecutivas (T0J0 y T2J2).
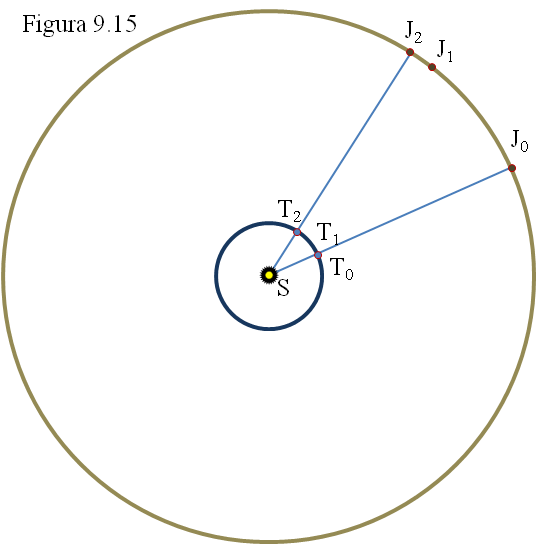
Comenzamos en una oposición de Júpiter (T0J0). Un año después la Tierra ocupará la misma posición (T1) mientras que Júpiter habrá avanzado un poco menos de un doceavo de su órbita y se situará en J1. Algo después, unos 34 días, se produce la siguiente oposición en T2J2. En 398,9 días la Tierra ha avanzado
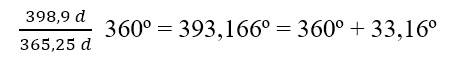
Y en esos mismos 398,9 días Júpiter recorrerá
El acuerdo es casi perfecto. Esta relación entre los períodos sidéreo, sinódico y el año terrestre ya había sido detectada antes de Copérnico, pero no tenía una razón de ser dentro del sistema ptolemaico.
Distancias
La máxima elongación de Venus es de 47º. Sólo con este dato Copérnico pudo calcular la proporción entre las distancias Sol-Tierra y Sol-Venus.
Ejercicio 9.4
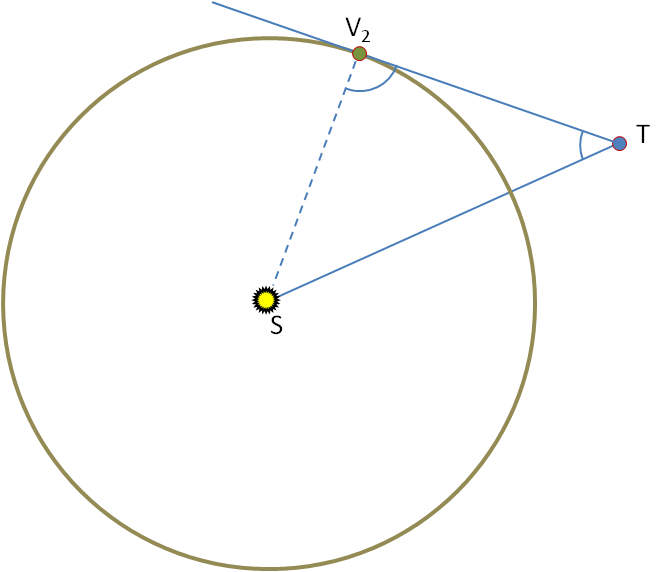
En el momento de la máxima elongación (V2, por ejemplo) la recta TV2 es tangente a la circunferencia que recorre Venus. ¿Cuánto tiene que medir el ángulo SV2T que forman la tangente TV2 y el radio SV2? Ya sabemos que el ángulo STV2 = 47º. ¿Cuánto tiene que medir el tercer ángulo, el TSV2?
Ahora sabemos que la distancia Tierra – Sol es de 150 millones de km, así que en el triángulo STV2 conocemos los tres ángulos y un lado. Tenemos datos suficientes para calcular la longitud SV2, bien por semejanza, bien utilizando trigonometría.
Por semejanza, que requiere menos matemáticas: dibuja un triángulo semejante al SV2T, de forma que el ángulo en T sea de 47º y que ST mida 15 cm. ¿Cuánto mide en él el lado SV2? ¿Cuál es la distancia de Venus al Sol, es decir, el radio de su órbita?
Haz clic aquí para ver la solución
Ejercicio 9.5
La máxima elongación de Mercurio es de 23º por término medio (varía bastante, entre 18º y 27º). ¿Cuál es su distancia media al Sol?
Haz clic aquí para ver la solución
Ejercicio 9.6
Copérnico utilizó las cuadraturas y las oposiciones para averiguar la distancia Marte – Sol. Esperó a que Marte estuviera en oposición (T1M1) y contó el número de días que transcurrieron hasta la cuadratura inmediatamente siguiente (T2M2): pasaron 106 días.
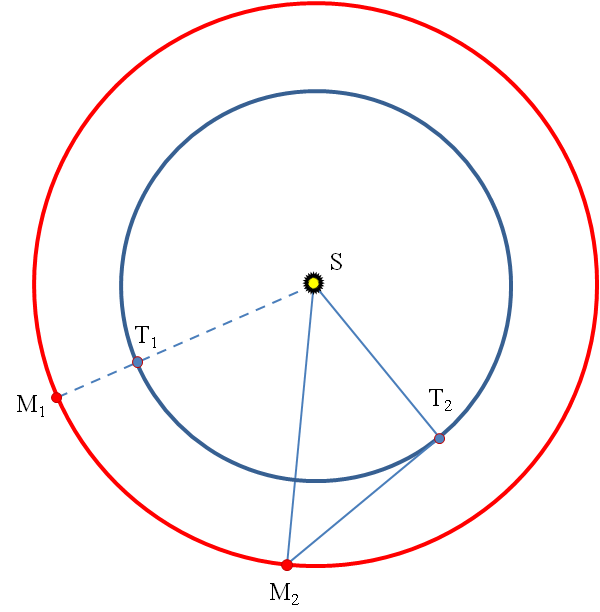Calcula el ángulo recorrido por la Tierra (T1ST2) y por Marte (M1SM2) en esos 106 días.- Halla, por diferencia de los dos anteriores, el ángulo T2SM2.
- ¿Cuánto valen los tres ángulos del triángulo ST2M2?
- Dibuja un triángulo semejante al ST2M2 de manera que ST2 mida 15 cm (recuerda que Tierra-Sol = 150 millones de km) y averigua la distancia Sol-Marte.
Haz clic aquí para ver la solución
De forma similar Copérnico calculó las distancias del Sol a Júpiter y a Saturno. Puedes ver todos los datos en la tabla que hay al final del tema. Posteriormente, con métodos más precisos, Giovanni Domenico Cassini en 1672 calculó la distancia Tierra-Marte y Edmund Halley en 1716 midió la distancia Tierra – Sol. Si quieres saber más sobre estos cálculos históricos haz clic aquí.
Ejercicio 9.7
- Calcula la velocidad a la que se mueve la Tierra mientras recorre su órbita. Para ello halla la distancia que recorre en un año, es decir, la longitud de su órbita (hazlo como si fuera una circunferencia exacta), y divídela por el tiempo que tarda. Expresa la velocidad en km/s.
- Haz lo mismo con los demás planetas hasta Saturno. Los datos que te hagan falta los encontrarás en la tabla del final del tema. Expresa siempre la velocidad en km/s. ¿Qué planetas son más rápidos, los interiores o los exteriores?
Haz clic aquí para ver la solución