9.4 Trabajos escolares
Poster a escala del Sistema Solar
Vas a confeccionar un dibujo en el que queden representadas las órbitas de los planetas a escala. Para ello consigue una cartulina de 50×70 cm, colócala apaisada y traza una recta en su centro, a 25 cm de cada borde. Haz una marca sobre esta recta a 10 cm del extremo izquierdo. Es la posición del Sol. Para señalar la posición y dibujar las órbitas de los planetas vas a utilizar la escala 1 cm (en el mural) = 50 millones de km (en la realidad). Calcula la distancia (en cm) que le corresponde a cada planeta según los datos de la tabla final.
Para dibujar las órbitas traza, con el compás o con un hilo, circunferencias con centro en el Sol. Te caben completas las órbitas hasta Marte. Las de Júpiter, Saturno y Urano sólo entran parcialmente.
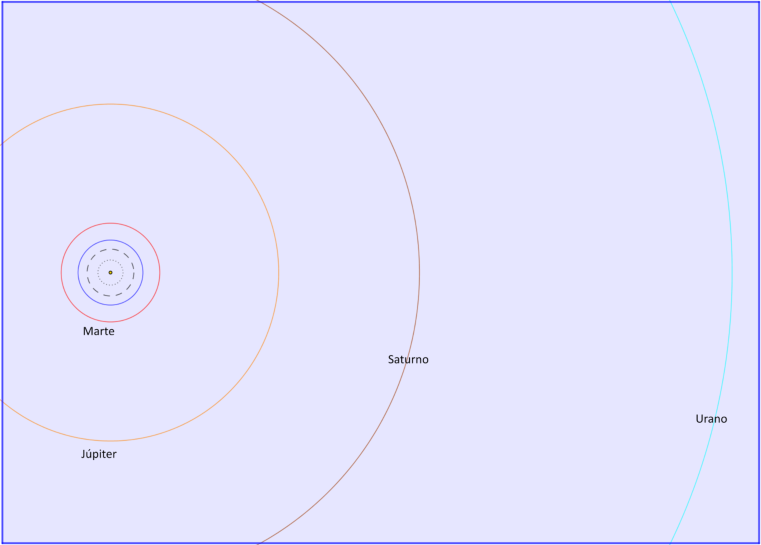
Modelos a escala
La interiorización de las distancias astronómicas es difícil. Sus enormes valores alejados de nuestra experiencia cotidiana hacen muy complicado que nos hagamos una idea cabal de las dimensiones del sistema solar. Los modelos o maquetas a escala, asociados a objetos comunes, pueden servir para hacernos más asequibles esos tamaños.
- Vamos a situar al Sol en Madrid, en su centro clásico y punto 0 del kilometraje de las carreteras que es la Puerta del Sol. Y situaremos los planetas a lo largo de la carretera A 2 en dirección a Barcelona. Usaremos esta escala: 1 km en la carretera va a representar 10 millones de km en la realidad. Así, la Tierra estaría a 15 km y los demás planetas a las distancias indicadas en la tabla:
Mercurio 5,8 Madrid Venus 10,8 Barajas Tierra 15 San Fdo. de Henares Marte 22,8 Torrejón de Ardoz Júpiter 77,8 Trijueque Saturno 142,9 Medinaceli Urano 287,5 Épila Neptuno 450,4 Alcarrás
Se puede dibujar esta carretera sobre una cartulina, como se puede ver en la fotografía, e indicar en ella las posiciones de los planetas, su distancia a la Puerta del Sol, así como la población en la que se situaría. O hacer una maqueta sobre una plancha de aglomerado, con un poco más de arte y de gracia, más adecuada para los pequeños. - O también se podría construir una maqueta o un mural en una ciudad como Madrid, con nuestra estrella de nuevo en la Puerta del Sol y una escala de forma que Neptuno quede a unos 9 km. Precisar el lugar en el que se encontrarían los planetas, quizá a lo largo de una calle, como la de Alcalá. Esta sería una tabla con las distancias:
Mercurio 119 m Puerta del Sol con Alcalá Venus 216 m Alcalá 9, Ministerio de Hacienda Tierra 300 m Alcalá 13, Real Academia de Bellas Artes de San Fernando Marte 456 m Alcalá 25, metro Sevilla Júpiter 1,56 km Alcalá 81, metro Retiro Saturno 2,86 km Alcalá 157, metro Goya Urano 5,75 km Alcalá 389, metro Pueblo Nuevo Neptuno 9 km Alcalá 625, metro Canillejas Siguiendo la misma escala, la estrella más próxima, α Centauro que está a 4,3 años luz se situaría en ese modelo nada menos que a ¡80.000 km! la quinta parte de la distancia Tierra – Luna.
- O en un pasillo largo del centro escolar, con murales de cada planeta a la distancia que les corresponda a escala. Quizá estaría bien incluir el tamaño de los planetas, poniendo en el mural un dibujo a escala, o colgando del techo una bola al tamaño correspondiente. La idea de la carretera Madrid – Barcelona (apartado A) podría quizá ilustrarse también en ese pasillo. En todo caso habrá que adaptar la escala a la longitud de que dispongamos.
La danza de los planetas
En el patio del centro escolar, o en un terreno despejado de unos 25×25 m, dibujaremos a escala las órbitas de los planetas y señalaremos, para cada uno de ellos, la distancia que recorre en una semana de manera que cada órbita quede jalonada por una serie de marcas que indican la posición del planeta de semana en semana.
Trazaremos las órbitas (con tiza, cinta aislante, pintura, o lo que nos parezca) como circunferencias con centro en el Sol, pues no necesitamos precisión. Podemos utilizar una cuerda. Con una cinta métrica, o con una cuerda con dos nudos a la distancia adecuada, vamos recorriendo cada órbita señalando en ella las posiciones semanales. A partir de Júpiter el movimiento es tan lento que proponemos hacer una marca cada diez semanas, y no hace falta completar toda la circunferencia, bastará dibujar unas pocas (diez o quince).
Colocamos un alumno en cada órbita y vamos marcando el ritmo de avance con un tambor, un silbato, etc. Cada alumno debe avanzar por su órbita de marca en marca con cada señal simulando de esta manera los movimientos del sistema solar. El alumno-Júpiter y el que haga de Saturno (si es que nos da el patio para tanto) deben avanzar una marca cada diez señales; lo mejor es que vayan poco a poco, contando mentalmente, para llegar a la siguiente marca en el momento adecuado. Con un poco de ensayo esto sale perfecto.
Tabla con los datos necesarios: R = radio de la órbita
L = avance semanal (los que llevan * es cada 10 semanas)
Una vez puesto en marcha todo el mecanismo es posible pararlo cuando nos interese para hacer ver diferentes posiciones de interés (conjunciones, oposiciones); también puede simplificarse y poner en marcha solo dos planetas (la Tierra y Marte, por ejemplo) y analizar con algo de detalle lo que pasa, lo que se ve desde nuestro planeta.
| Planeta | R (m) | L (cm) |
| Mercurio | 0,77 | 37 |
| Venus | 1,45 | 28 |
| Tierra | 2 | 24 |
| Marte | 3,05 | 20 |
| Júpiter | 10,4 | 105* |
| Saturno | 19,1 | 78* |
Visibilidad de los planetas
Para mostrar qué planetas van a poderse observar nada más anochecer, cuáles están por encima del horizonte toda la noche o los que solo podrán verse poco antes del alba, se puede construir algo análogo al “temporizador” que utilizamos para la Luna. Necesitamos de todas formas conocer de antemano la elongación de cada planeta para poderlos situar debidamente. Esta elongación hay que obtenerla de alguna revista especializada, páginas web de efemérides astronómicas o de algún programa informático.
Una vez conocida la elongación de cada planeta los podemos situar en la plantilla de la figura superior. Ésta debe poder girar por detrás de un horizonte.
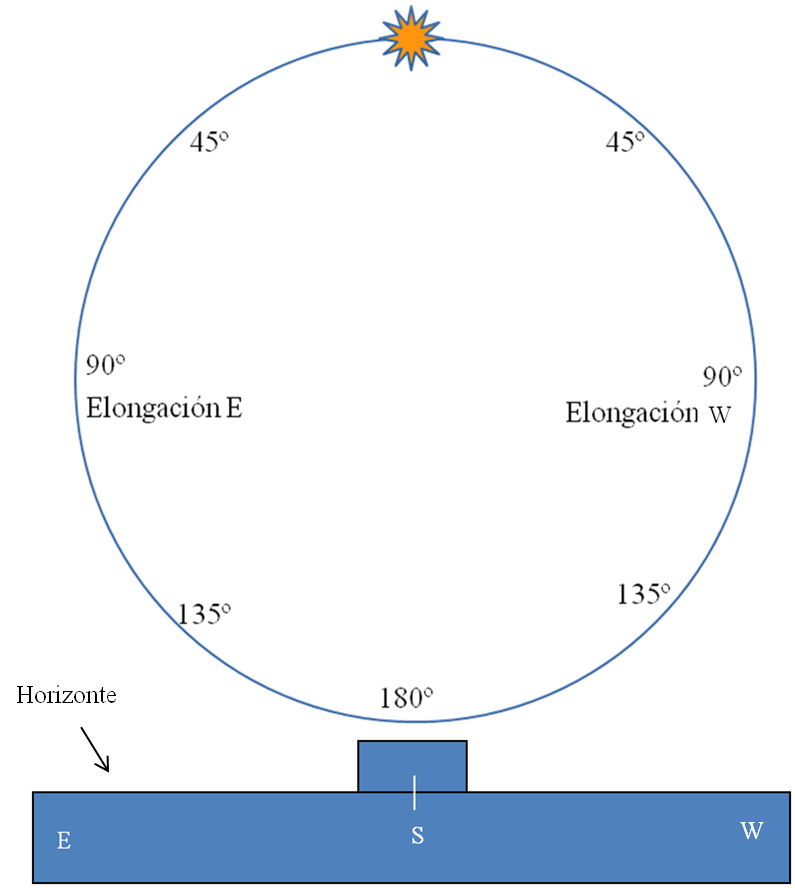
Haz clic aquí para poder imprimir ambas plantillas
Por ejemplo con los datos indicados en la tabla adjunta resultaría la plantilla de la figura inferior. Si superponemos la plantilla al horizonte y la vamos girando podemos analizar qué planetas serán visibles a diferentes horas. Al atardecer, como se observa con el Sol al W, sólo serán visibles Saturno (hacia el SW y ya próximo a ponerse) y Marte (hacia el S, muy alto); Mercurio, tan cerca del Sol será indetectable.
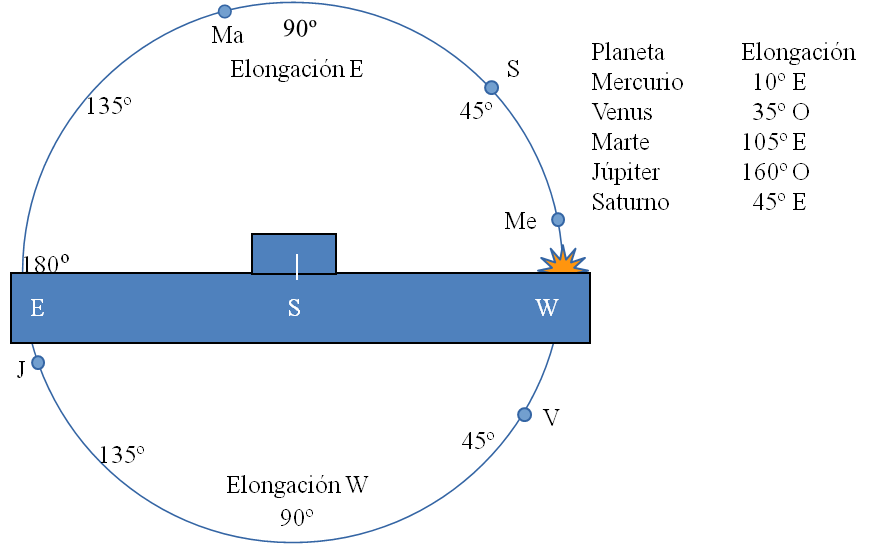
A medianoche ya Marte estará a punto de ponerse, pero Júpiter brillará bien alto en el cielo S.
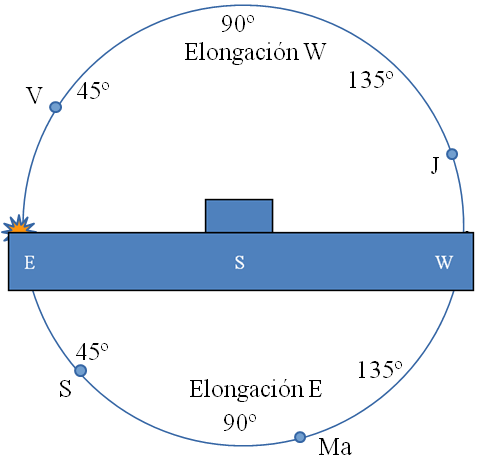
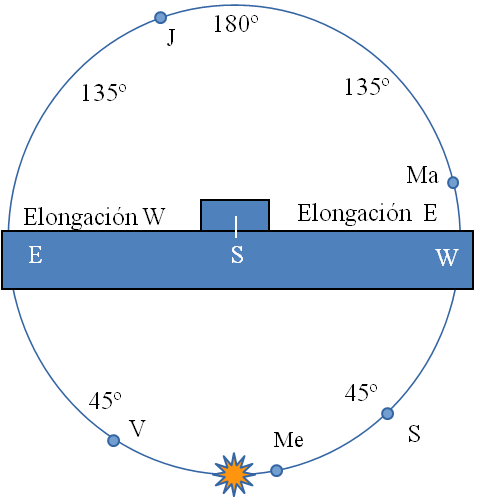
Por último, poco antes del amanecer Júpiter aún será visible, bajo y hacia el W, pero por el horizonte E podremos ver al lucero del alba, Venus, que sale algo antes que el Sol.
Órbitas de la Tierra y Marte a escala
En la figura siguiente están dibujadas las órbitas de la Tierra en azul y de Marte en rojo tal y como son realmente, a escala, con su orientación, sus focos, el perihelio Π de cada uno y sus posiciones de mes en mes, contadas a partir del perihelio. Para la Tierra hay 12 puntos, uno por mes, y para Marte hay 23 puntos. Dado que Marte recorre su órbita en 687 días (que son unos 22 meses y medio) el último tramo (entre la posición 22 y Π) no corresponde a un mes sino solo a unos 16 días.
Puedes fotocopiarla en una cartulina grande o en una hoja de formato DIN A3 para verla bien y poder analizar algunas cuestiones. Haz clic aquí para imprimirla
Observa que los dos focos de la órbita terrestre (el Sol y el cercano punto azul) son casi coincidentes, mientras que los focos de la órbita marciana sí que tienen una separación bien perceptible.
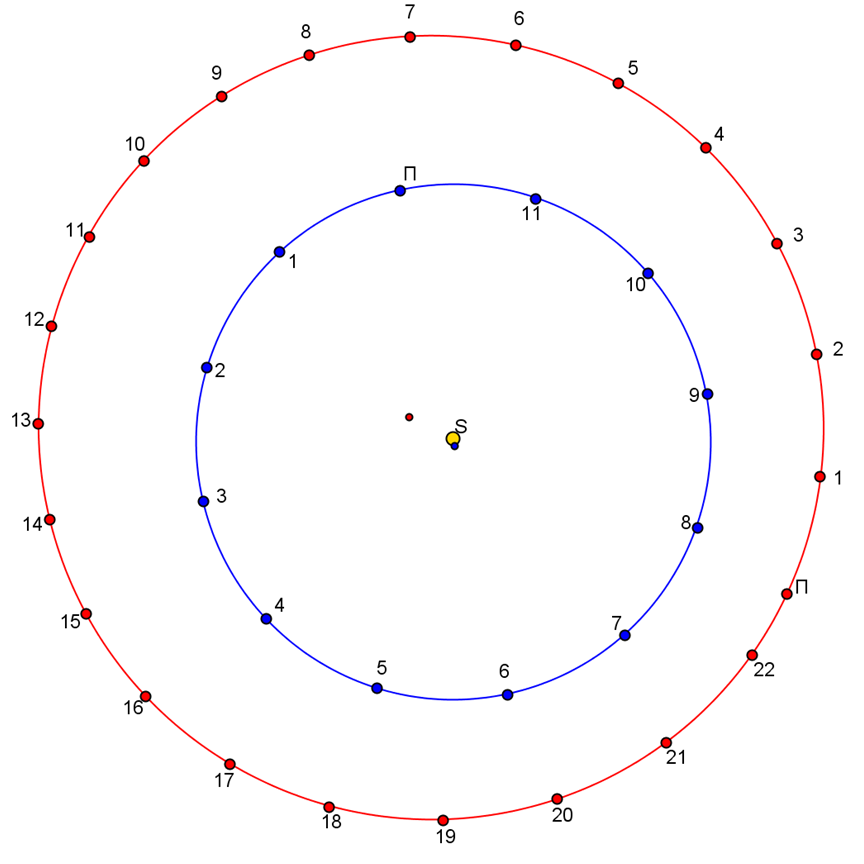
Fíjate ahora en que, mientras el avance de la Tierra es prácticamente regular y uniforme, el de Marte en cambio sí que varía notablemente. Puedes medir la distancia en los tramos Π-1 (cerca del perihelio) y 11-12 (próximos al afelio) y apreciar que la primera es considerablemente mayor que la segunda. Pero los tramos mensuales marcianos son siempre más cortos que los terrestres: Marte tiene menor velocidad orbital.
También puedes buscar posiciones destacadas (oposiciones, cuadraturas, conjunciones). Por ejemplo en T2-M12 hay una oposición, en T10-M7 Marte se presenta en cuadratura (Oeste) y en T9 – M14 tendríamos una conjunción.
El mejor momento para observar al planeta rojo es en su oposición pues entonces Marte está más cerca de nosotros y lo veremos más brillante y aparentemente más grande. Sin embargo la oposición puede producirse en cualquier lugar de sus órbitas, como en T2-M12, pero también podría ocurrir aproximadamente en T9-M2, y esas mínimas distancias oscilan apreciablemente dada la excentricidad de la órbita marciana. Por eso hay oposiciones especialmente “buenas”, como la T9-M2, si Marte está próximo a su perihelio.
Mercurio y la 2ª ley de Kepler
La órbita de Mercurio es la que tiene mayor excentricidad de todas y por ello resulta muy llamativa la gran variación de su velocidad orbital, como se muestra en la figura inferior. S es el Sol, F el otro foco, C el centro, Π el perihelio y A el afelio. Se ha dibujado una circunferencia (punteada en rojo) de centro C y radio la distancia media de Mercurio al Sol (el semieje mayor de la elipse). ¡Sigue siendo casi, casi igual que la elipse! Los 12 puntos sobre la órbita corresponden a posiciones del planeta igualmente espaciadas en el tiempo (poco más de una semana de una a otra).
Puedes fotocopiarlo en grande o dibujarlo en una cartulina o incluso se podría dibujar en un gran mural o en el suelo del aula.
Haz clic aquí para imprimirla
Con un transportador puedes medir el ángulo (siempre con vértice en S) avanzado por Mercurio en cada semana. Comprobarás que cerca del perihelio se mueve más del doble de deprisa que en las cercanías del afelio.
Mural o maqueta de una retrogradación de Marte
Aquí tienes de nuevo las órbitas de la Tierra y de Marte a escala y con todas sus proporciones reproducidas fidedignamente (salvo la inclinación relativa de ambos planos orbitales). Las posiciones representadas son simultáneas (es decir, cuando la Tierra estaba en 1, Marte también se encontraba en su posición 1) y centradas en la oposición (posiciones 5 de ambos).
Haz clic aquí para imprimirla
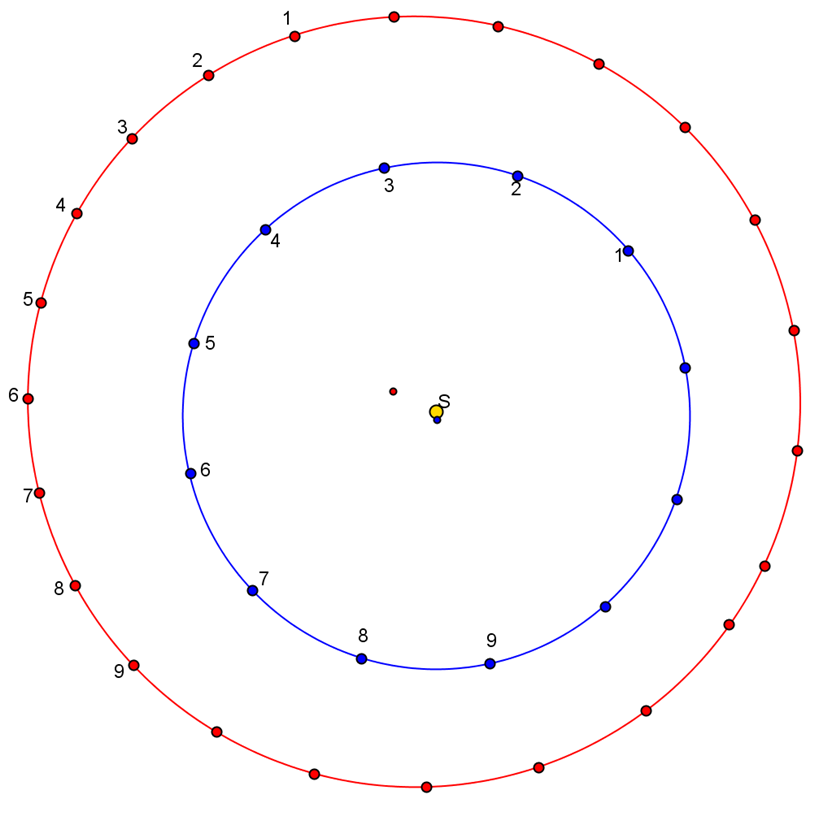
Haz una fotocopia en una hoja DIN A3, pégala sobre una plancha de cartón pluma o similar y colócala sobre un pupitre en el extremo del aula más alejado de la pizarra. Hazlo de forma que la línea recta Sol- T5 – M5 se dirija en perpendicular a la pizarra.
Con un hilo fino muy largo (los de coser suelen funcionar bien) une las posiciones simultáneas (T1 – M1 por ejemplo). Puedes clavar un alfiler en T1, atar allí el hilo y, haciendo que pase por la posición M1, desenrolla el hilo y haz que llegue hasta la pizarra, marca allí el punto donde estaría Marte visto desde la Tierra. La pizarra hace el papel del lejano telón de fondo de las constelaciones.
Haz lo mismo con las demás posiciones (T2 – M2, etc.), como en la figura 9.12. En la pizarra verás aparecer, no el clásico bucle o lazo, puesto que hemos puesto las dos órbitas como si estuvieran en el mismo plano, pero sí un claro movimiento de vaivén, un avance de derecha a izquierda, un momentáneo retroceso y una vuelta a la marcha habitual.