La escala de magnitudes

Desde la Tierra las estrellas se ven con diferente brillo: las hay de 1ª magnitud, de 2ª, de 3ª, etc. Ésta es la magnitud aparente (m). Hay algunas estrellas, como Capella, tan brillantes que su magnitud aparente es 0. Sirio, la más brillante del cielo terrestre, es de magnitud -1,5.

El primer astrónomo que asignó sistemáticamente valores numéricos a cada estrella en función de su brillo fue Claudio Ptolomeo (siglo II de nuestra era), en su gran obra El Almagesto, aunque se sospecha que esta clasificación pudo haber sido ideada anteriormente por Hiparco de Nicea (siglo II a.C.) Los libros VII y VIII del Almagesto contienen el primer catálogo estelar riguroso, de unas mil estrellas, y a cada una se le asigna una magnitud numérica, desde la 1 hasta la 6, sistema que se ha mantenido hasta la actualidad (¡desde hace casi 2.000 años!) y que seguimos utilizando aunque ampliándolo (con magnitudes negativas y mayores que 6) y ajustándolo a criterios físicos más precisos que la mera percepción de nuestros ojos (figura 14.2).

¿Cuánto más brillante es una estrella de magnitud 1 que otra de magnitud 2? Se ha comprobado que cada salto de una magnitud corresponde a un aumento o disminución del brillo en un factor fijo. Para que se entienda: una estrella de magnitud 1 es f veces más luminosa que otra de magnitud 2. Pero una estrella de magnitud 2 también es f veces más luminosa que una de 3, etc. Y la de 1ª magnitud será por tanto f · f = f ² veces más brillante que una de 3ª. Esta tabla quizá sirva para ilustrarlo.

Magnitud	1	2	3	4	5	6
Brillo	B·f 5	B·f 4	B·f 3	B·f 2	B·f	B

¿Y cuál es el valor de ese factor f que acaba de aparecer? En1856 el astrónomo británico Norman Pogson formalizó el sistema definiendo que una estrella de primera magnitud es 100 veces más brillante que una de la sexta magnitud. Así que f ⁵ = 100, por lo que:

Así Alkaid (m = 2) es 2,512 veces más brillante que la bella doble Albireo (β Cygni, m = 3), Spica (m = 1) será 2,512³ ≈ 16 veces más brillante que una estrella de la 4ª magnitud, como Thuban (α Draconis, la que fue estrella polar en tiempos de los faraones egipcios) puesto que desde m = 1 hasta m = 4 hay un salto de 3 unidades.

Ejercicio 14.2

1. ¿Cuántas veces es más brillante una estrella de 1ª magnitud que otra de 3ª? ¿Y una de 3ª que otra de 6ª?
2. Suponiendo que la Luna llena es de magnitud -13 y el Sol -27 y, ¿cuántas veces es más brillante éste que aquella?

Haz clic aquí para ver la solución.

 

Pero ¿por qué aparece tan brillante Sirio? ¿Porque es una estrella muy luminosa o porque está muy cerca de la Tierra? ¿Son todas las estrellas igual de luminosas y su brillo aparente sólo es efecto de su distancia?

Es lógico suponer que las estrellas no tienen por qué ser todas exactamente igual de potentes. Se sabe que, en efecto, las hay muy luminosas (mucho más que nuestro Sol) y otras, mucho menos potentes, que emiten al espacio bastante menos luz y calor que el Sol. Sirio aparece tan brillante porque está muy cerca de la Tierra, pero no es una estrella extraordinaria. En cambio Deneb, que parece menos brillante que Sirio, es más luminosa, más potente, pero está mucho más lejos.

Sería interesante conocer cuál es la luminosidad verdadera de las estrellas, su luminosidad o potencia intrínseca, que queda enmascarada por el efecto producido por su distancia a la Tierra. Por eso se define magnitud absoluta (M) como la magnitud aparente con la que observaríamos una estrella si estuviera situada a una distancia de 10 parsecs es decir 32,6 años luz. Pero, claro, no somos capaces de mover las estrellas a nuestro antojo y situarlas a esa distancia de 10 pc. ¿Qué podemos hacer?

Pues resulta que, en algunos casos, es posible averiguar directamente cuál es la magnitud absoluta de una estrella. Esto se consigue analizando la luz que nos llega de ella mediante instrumentos especiales, como el espectroscopio y utilizando diversos resultados teóricos de la Física estelar (tema 15). Conocida esta magnitud absoluta, así como la magnitud aparente (conocida para todas las estrellas), es posible deducir de estos dos datos cuál es la distancia a esa estrella. Así se dispone de otro método para calibrar las distancias.

Si quieres saber la relación matemática entre la magnitud absoluta y la relativa pulsa aquí.

En la figura 14.3 hay una serie de líneas horizontales, otras verticales y otras oblicuas. El eje horizontal corresponde a las distancias, expresadas en años luz (en azul y con escala logarítmica). En el eje vertical está situada la magnitud aparente (abajo las estrellas menos brillantes, vistas desde la Tierra, y arriba las más brillantes, que tienen magnitud aparente negativa). Las líneas oblicuas (en rojo) señalan la magnitud absoluta.

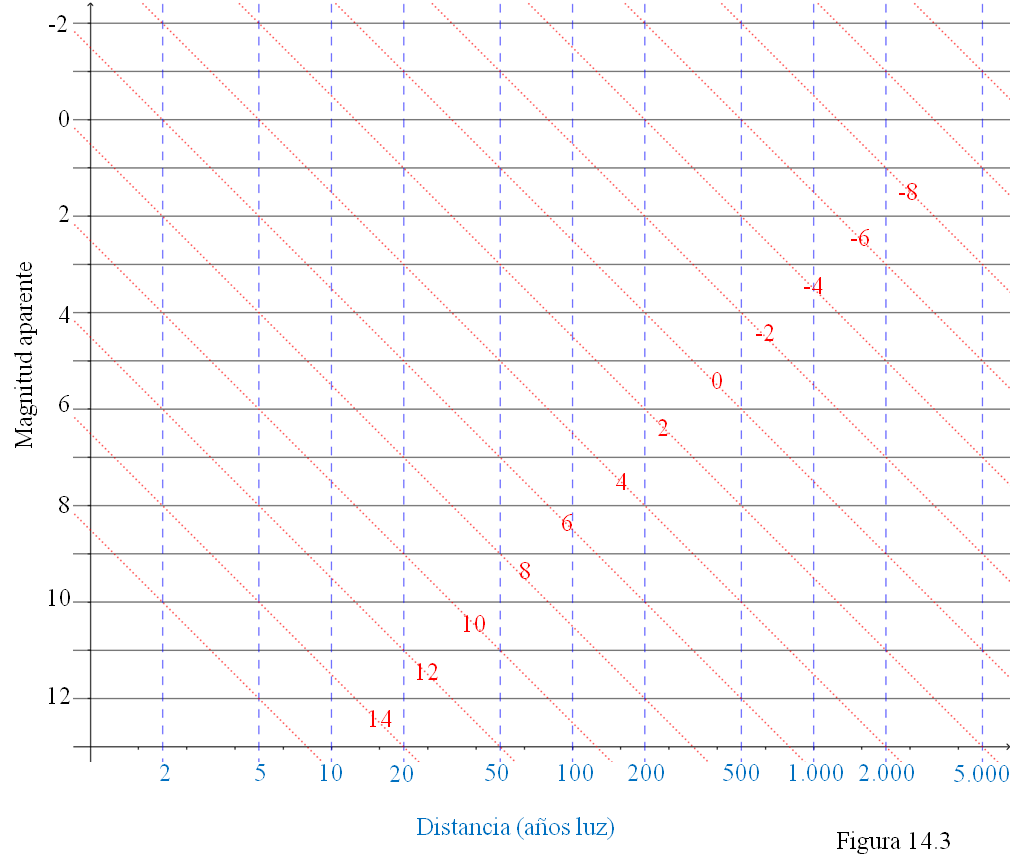
Conociendo la magnitud aparente y la distancia de una estrella, podemos marcar un punto en la figura 14.3 que señale la posición de la misma. Para averiguar su magnitud absoluta tenemos que localizar cuál es la línea oblicua que queda más cerca de esa estrella. Sirio, por ejemplo, tiene una magnitud aparente de -1,5, así que está en una línea horizontal intermedia entre -1 y -2, en la parte más alta de la lámina. Su distancia es de 8,8 años luz por lo que estará en una línea vertical un poco a la izquierda de la correspondiente a 10 años luz. El punto resultante está entre la línea oblicua señalada con un 0 y la de 2, más cerca de esta última. Eso quiere decir que la magnitud absoluta de Sirio es aproximadamente 1,3, es decir, que se trata de una estrella “sólo” de 1ª magnitud que percibimos con mayor brillo del que le corresponde a causa de su proximidad a nosotros.

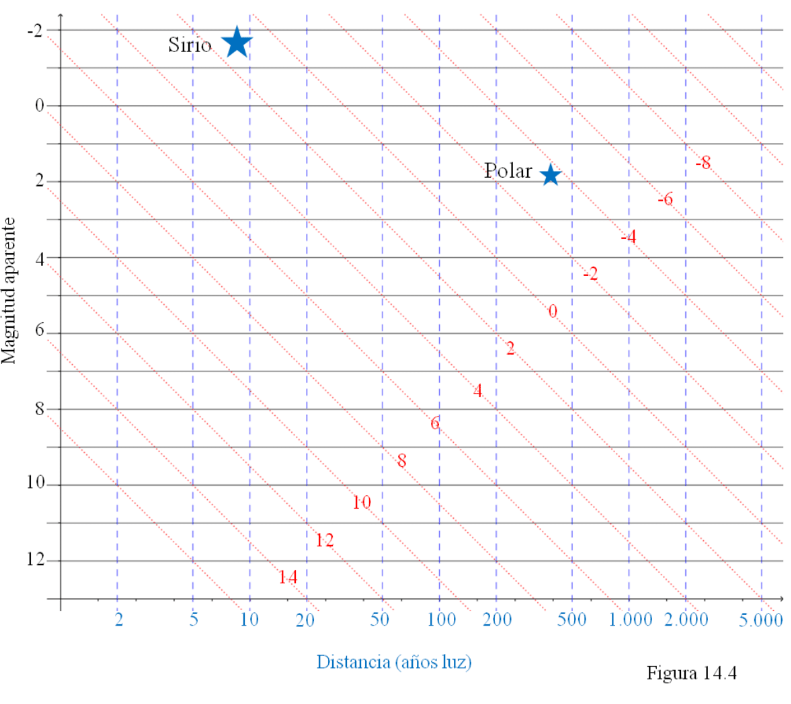
Y lo que nos interesa ahora es el proceso inverso: si conocemos de una estrella sus magnitudes aparente (m) y absoluta (M) también podremos situar esa estrella en el diagrama y obtener de él su distancia. Por ejemplo, la estrella Polar tiene m = 1,95 y se ha podido determinar a partir de su espectro que tiene una M = -3,66. La situamos en el diagrama (figura 14.4) y vemos que su distancia debe ser de unos 425 años luz.

Ejercicio 14.3

Utilizando la figura 14.3, completa la tabla que relaciona magnitudes aparentes, absolutas y distancias. Haz clic aquí para imprimar la gráfica

 

Estrella	m	Distancia (a.l.)	M		Estrella	m	Distancia (a.l.)	M
Sirio	-1,5	8,8			Deneb	1,2		-7
Arturo	0,15	37			Regulus	1,3		-0,6
Vega	0	25			Sirio B	8,4	8,8
Rigel	0,15	863			Procion B	10,8	11,4
Antares	1	554			Barnard	9,5	6
Spica	1	250			61 Cygni	5,2	11,4
Aldebarán	0,85	67			Castor	2		1
Pollux	1,15	34			Alkaid	1,85		-0,7
Capella	0		-0,6		Rasalhague	2		1,3
Altair	0,75		2,2		η Casiopea	3,5		4,6

Haz clic aquí para ver la solución

 

Ejercicio 14.4

Utilizando la expresión final que aparece en la ampliación citada, revisa tus resultados del ejercicio 14.3

Haz clic aquí para ver la solución