9.3 Las leyes de Kepler
A lo largo del siglo XVII aparecieron otras dos obras capitales en la Historia de la Astronomía. La primera, en 1609, fue Astronomia Nova del genial y apasionado Johannes Kepler. Mucho menos famosa y reconocida que las otras que hemos citado y citaremos en este capítulo, en ella se enuncia la primera ley del movimiento planetario y se esboza la segunda.
- 1ª ley: Los planetas describen órbitas elípticas con el Sol en uno de los focos.
Esto destrozaba uno de los dogmas establecido como inamovible durante esos 2.000 años de estudios e investigaciones: la circularidad de los movimientos celestes.
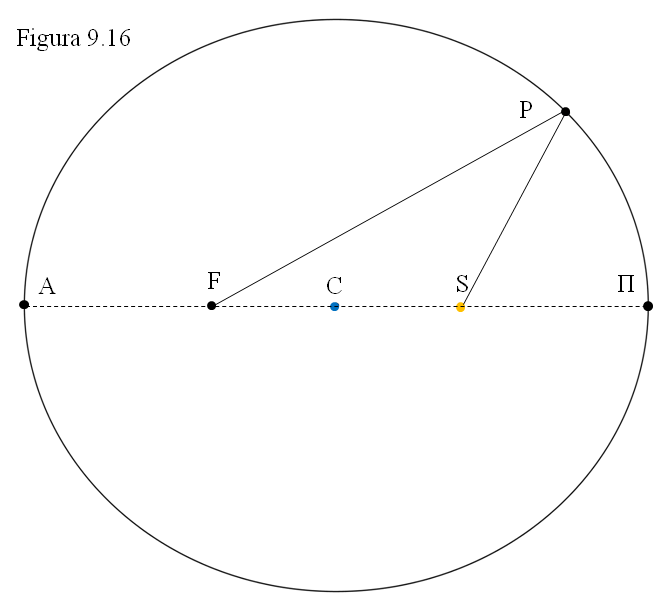
Una elipse es una circunferencia “achatada” caracterizada por sus dos focos (F y S en la figura 9.16) de forma que para cualquier punto P de la curva la suma de distancias SP + FP se mantiene siempre igual. El punto medio entre los dos focos es el centro C de la elipse y la línea AΠ su eje mayor. En uno de los focos (S) se encuentra el Sol y en el otro (F) no hay nada. El “achatamiento” o más concretamente la excentricidad (e) depende de la separación de los focos, de su distancia al centro. Es la relación e = CS/CA, de tal forma que 0 < e < 1.
Como consecuencia, la distancia de cada planeta al Sol es variable, en mayor o menor medida según la excentricidad. El punto más próximo se llama perihelio Π, y el más lejano afelio A. En esta figura, la clásica en los libros de texto y de divulgación, es engañosa. En ella se representa una elipse de e = 0,4 (porque la distancia CS es el 40% de la longitud CΠ). La excentricidad de las órbitas planetarias es mucho menor con lo que los focos están mucho más cercanos que en esa figura y la órbita se parece demasiado a una circunferencia.
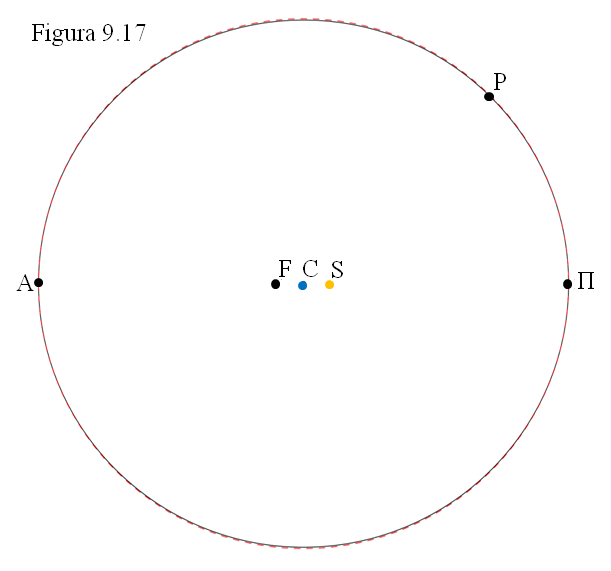
La figura 9.17 corresponde a la órbita de Marte (excentricidad 0,1 es decir CS es el 10% de CΠ) dibujada en negro con trazo continuo.
En rojo y trazo discontinuo está dibujada una circunferencia de centro C y radio CΠ. Apenas se diferencia de la elipse.
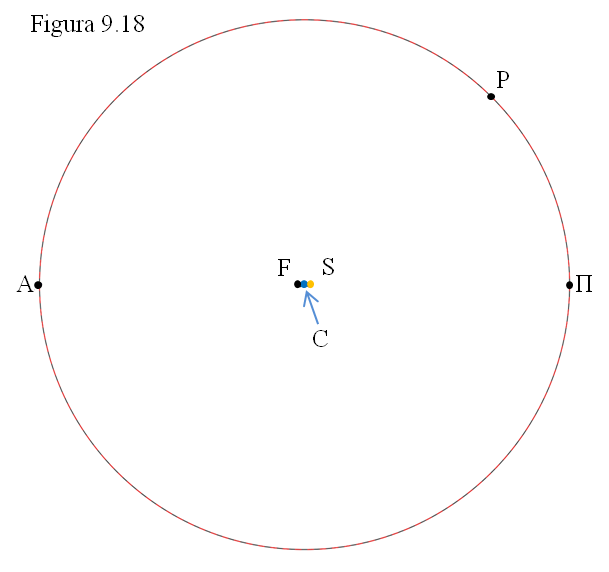
Y no digamos para la órbita terrestre en la que CS es solo un 1,7% de CΠ (e = 0,017). En este caso la órbita elíptica y la circunferencia son absolutamente indistinguibles. Por eso costó tantos siglos romper con la creencia en la circularidad de las órbitas. Sin embargo las distancias mínima y máxima de la Tierra al Sol sí varían un poco; la distancia media (CΠ) es de unos 150 millones de km; la mínima en el perihelio (SΠ) es de 147,45 y la máxima (en el afelio) SA = 152,55, figura 9.18.
El perihelio terrestre ocurre el día 4 de enero. ¡En pleno invierno (en el hemisferio Norte) es cuando la Tierra está más cerca del Sol!
Y el afelio el 4 de julio. Como ya vimos antes, el ciclo de las estaciones no está causado por la diferente distancia de la Tierra al Sol (que tiene muy poca variación) sino por la inclinación con la que los rayos solares inciden sobre la superficie terrestre.
Cada órbita planetaria está en un plano que pasa por el Sol; pero no están todos en el mismo sino que tienen ligeras inclinaciones; el nuestro es el plano de la eclíptica que es el que se toma como referencia y esas ligeras inclinaciones de los otros planos hacen que veamos a los planetas a veces algo “por encima” de la eclíptica y otras un poco al Sur.
- 2ª ley: El planeta recorre su órbita de forma que el segmento Sol – Planeta barre áreas iguales en tiempos iguales.
Para ilustrar esta ley mostramos en la figura 9.19 la órbita de Mercurio que es el planeta con mayor excentricidad de todos (0,2). Fíjate que los focos están bastante separados, a pesar de lo cual la elipse se sigue pareciendo mucho, mucho a una circunferencia. De P a P’, tanto a la izquierda como a la derecha, transcurre una semana; según esta 2ª ley los triángulos sombreados SPP’ tienen que tener la misma área. En las proximidades del perihelio (a la derecha), al ser sensiblemente menor la distancia SP, el triángulo SPP’ tiene que ser más “alto” que el de la izquierda (cerca del afelio), es decir, el planeta tiene que avanzar más deprisa. Para Mercurio, el avance en una semana cerca del perihelio es de 45,6º, mientras que también en una semana pero ahora cerca del afelio tan solo recorre 20,5º.
En esta animación se observa cómo el área se mantiene constante mientras que el arco avanzado por el planeta va oscilando desde un máximo en las proximidades del perihelio hasta un mínimo cerca del afelio.
Esta ley permite el cálculo preciso de las posiciones planetarias, aunque exige matemáticas de cierta envergadura. Las predicciones obtenidas con ella concuerdan ya con magnífica precisión con las observaciones hechas para comprobarlo.
La siguiente animación muestra el movimiento real de un planeta P; se ha añadido un punto M que recorre la órbita con velocidad constante para que se observe cómo P a veces va un poco más deprisa y adelanta M y en otras partes de la órbita (cerca del afelio) se frena y va por detrás de M.
La 2ª Ley de Kepler es una consecuencia de la Ley de la Conservación del Momento Angular, si quieres saber más sobre este hecho haz clic aquí. Al mismo tiempo, como hemos visto los planetas tienen órbitas elípticas, sin embargo las trayectorias de otros cuerpos que se mueven bajo la atracción gravitatoria del Sol pueden ser diferentes. Para saber más haz clic aquí.
- 3ª ley: El cuadrado del período de traslación (T) de cada planeta es proporcional al cubo de su distancia media (a) al Sol: T2 / a3 = K = cte.
Encontrada por Kepler de forma empírica establece una relación numérica entre la distancia al Sol y el periodo de traslación del planeta. Si quieres saber cómo se puede deducir el valor de la constante k haz clic aquí.
Ejercicio 9.8
Vas a comprobar la 3ª ley de Kepler. Expresa los períodos de traslación (T) de Venus y de Marte en años (687 días = 687/365.25 = 1.88 años, para Marte). Para las distancias medias al Sol (a) vas a hacer lo mismo: exprésalas en relación a la distancia media de la Tierra al Sol, que tomamos como unidad y que se llama Unidad Astronómica (UA). Para Venus, por ejemplo, a = 108·106 km = 108·106/150·106 UA = 108/150 UA = 0.72 UA.
Comprueba que para ambos planetas el cociente T2/a3 es aproximadamente igual a 1. Esto es lo que tiene que ocurrir siempre que expresemos T en años y a en unidades astronómicas.
Haz clic aquí para ver la solución
Todas las leyes de Kepler fueron encontradas por él de forma empírica, cotejando los datos de que disponía y buscando la mejor manera de ajustarse a ellos. No tuvieron justificación teórica hasta la llegada de otra de las cumbres científicas de todos los tiempos, los Philosophiae Naturalis Principia Mathematica (Principios Matemáticos de la Filosofía Natural), publicada por Isaac Newton en 1684 en la que establecía las leyes básicas de la Mecánica y la ley de la gravitación universal y deducía a partir de ellas las leyes de Kepler,
El siglo XVIII fue testigo de otro acontecimiento astronómico de primer orden: el descubrimiento de un nuevo planeta. En 1781 William Herschel, un músico alemán afincado como astrónomo en Inglaterra, detectó la presencia de un nuevo astro errante, Urano, que vino a sumarse a los conocidos desde la Antigüedad; el sistema solar crecía.
También en el XVIII se desarrolló un impresionante trabajo matemático para poder hacer frente a los retos que comportaban los cálculos de posiciones planetarias determinadas por las leyes de Kepler y de Newton, difíciles de tratar numéricamente. Fruto de ese desarrollo el francés Urbain Leverrier, estudiando las mínimas desviaciones observadas en las posiciones de Urano con respecto a lo previsto por las leyes y suponiendo que eran debidas a la existencia de otro planeta desconocido por el momento y aún más lejano, predijo teóricamente su posición. Asombrosamente Neptuno fue encontrado, en 1846, a solo 1º de la posición predicha por Leverrier: un triunfo clamoroso de la ciencia.
Ampliación: medida experimental de la velocidad de la luz
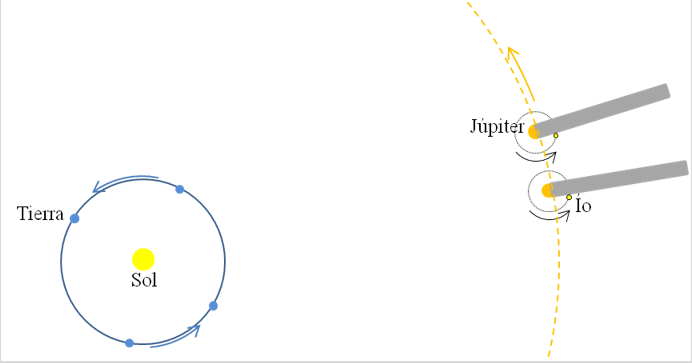
Olaff Rømer, astrónomo danés, era el ayudante de Giovanni Cassini en el Observatorio de París. En 1676 se dedicó a estudiar detalladamente el movimiento de Io, uno de los cuatro satélites de Júpiter descubiertos por Galileo en 1610. Era un movimiento casi circular y por tanto periódico. Se podía medir su periodo observando sus movimientos de salida de la sombra de Júpiter. Después de múltiples medidas dedujo que tardaba 42,5 h (poco más de día y medi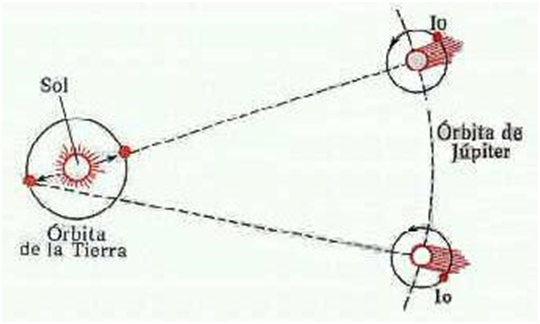o).
Pero algo no cuadraba; en algunos casos Io salía de la sombra de Júpiter más tarde de lo previsto, en otros lo hacía antes. ¿Era posible que Io no tardara siempre lo mismo en hacer ese recorrido? No tenía mucho sentido. Hasta que se percató que tardaba más cuando Júpiter y la Tierra estaban separándose, y menos cuando se aproximaban, ahí estaba la clave. En realidad esa diferencia se debía a la diferencia de espacio que debía de recorrer la luz en cada uno de los casos. Rømer estaba en condiciones de medir la velocidad de la luz.
Galileo lo había intentado midiendo la diferencia de tiempo de un suceso entre dos puntos situados a 1 kilómetro de distancia, pero se necesitaba una distancia muchísimo mayor, la que hay entre los planetas. Con los datos del desfase entre dos eclipses sucesivos de Io Rømer dedujo que la velocidad de la luz era de 225.000 km/s y estimó que ésta tardaría 11 minutos en llegar a la Tierra desde el Sol. Se equivocó por muy poco (en realidad son unos 8 minutos con 20 segundos), pero no por el método utilizado.
La tabla siguiente indica los principales datos orbitales de los planetas. El último dato corresponde a la inclinación del plano de giro del planeta con respecto a la eclíptica
| TABLA CON LOS PRINCIPALES DATOS ORBITALES DE LOS PLANETAS | ||||||||
| Mercurio | Venus | Tierra | Marte | Júpiter | Saturno | Urano | Neptuno | |
| P. orbital | 88 d | 225 d | 365 d | 687 d | 12 a | 29,4 a | 84 a | 164 a |
| P. sinódico | 116 d | 584 d | 780 d | 399 d | 378 d | 370 d | 367,5 d | |
| a (x106 km) | 58 | 108 | 150 | 228 | 778 | 1.429 | 2.875 | 4.504 |
| Excentricidad | 0,2 | 0,007 | 0,017 | 0,093 | 0,048 | 0,056 | 0,046 | 0,009 |
| Inclinación | 7o | 3,4o | 0o | 2o | 1o | 2,5o | 1o | 2o |